题目内容
9.解下列方程或不等式组(1)用配方法解方程:x2-x=3x+5
(2)解不等式组:$\left\{\begin{array}{l}{x+2>0}\\{3(x-1)+2≥2x}\end{array}\right.$,并判断-1,$\sqrt{3}$这两个数是否为该不等式组的解.
分析 (1)依据配方法步骤解答即可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原方程整理得:x2-4x=5,
∴x2-4x+4=5+4,即(x-2)2=9,
∴x-2=3或x-2=-3,
解得:x=5或x=-1;
(2)解不等式x+2>0,得:x>-2,
解不等式3(x-1)+2≥2x,得:x≥1,
∴不等式组的解集为x≥1,
∵-1<1,$\sqrt{3}$>1,
∴$\sqrt{3}$是该不等式组的解.
点评 本题主要考查解一元二次方程和解不等式组的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | -a+b+c+d=-(a-b)-(-c-d) | B. | x-(y-z)=x-y-z | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
 如图,C,D是线段AB上两点,D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长等于多少?
如图,C,D是线段AB上两点,D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长等于多少?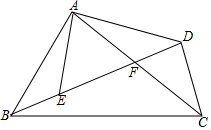 如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.
如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.