题目内容
4.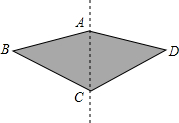 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
分析 根据题意滑翔伞的形状是左右成轴对称的四边形ABCD,得出∠D=40°,再利用四边形内角和定理求出∠BCD=360°-150°-40°-40°,即可得出答案.
解答 解:∵一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠D=∠B=40°,
∴∠BCD=360°-150°-40°-40°=130°.
故选C.
点评 此题主要考查了轴对称的性质以及多边形的内角和定理,利用四边形内角和定理是解决问题的关键.

练习册系列答案
相关题目
15.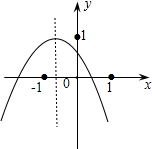 小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )
小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )
 小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )
小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.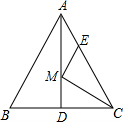 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )| A. | $\sqrt{26}$ | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{7}$ | D. | 4$\sqrt{2}$ |
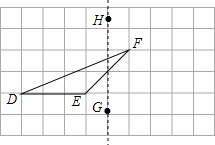 如图,在正方形网格上有一个△DEF.
如图,在正方形网格上有一个△DEF. 如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的度数为30度.
如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的度数为30度.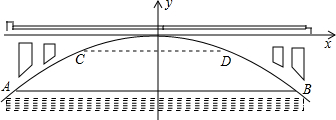
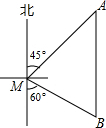 如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处,求渔船从A到B的航行过程中与小岛M之间的最小距离.(结果用根号表示)
如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处,求渔船从A到B的航行过程中与小岛M之间的最小距离.(结果用根号表示)