题目内容
16.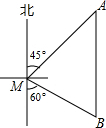 如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处,求渔船从A到B的航行过程中与小岛M之间的最小距离.(结果用根号表示)
如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处,求渔船从A到B的航行过程中与小岛M之间的最小距离.(结果用根号表示)
分析 过点M作MD⊥AB于点D,根据三角函数求出DM的长.
解答  解:过点M作MD⊥AB于点D,
解:过点M作MD⊥AB于点D,
∵∠AME=45°,
∴∠AMD=∠MAD=45°,
∵AM=180海里,
∴DM=AM•cos45°=90$\sqrt{2}$(海里).
答:渔船从A到B的航行过程中与小岛M之间的最小距离是90$\sqrt{2}$里.
点评 本题考查了解直角三角形的应用---方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
6.在画二次函数的图象时列出了下表:
观察表格,可以得到许多信息:
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-12;
(3)函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上有三点:A(m,y1)、B(m+1,y2)、C(m+2,y3).通过计算说明:(y3-y2)与(y2-y1)的差为定值.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 0 | 3 | 4 | 3 | 0 | -5 | … |
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-12;
(3)函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上有三点:A(m,y1)、B(m+1,y2)、C(m+2,y3).通过计算说明:(y3-y2)与(y2-y1)的差为定值.
4.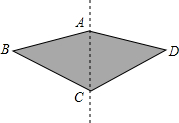 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
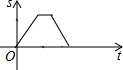
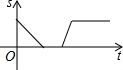
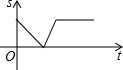
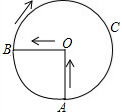 某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画出小江与中心O的距离S随时间t变化的图象是( )
某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画出小江与中心O的距离S随时间t变化的图象是( )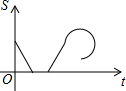
 已知A(1,2),B(m,$\frac{1}{2}$)是双曲线上的点.
已知A(1,2),B(m,$\frac{1}{2}$)是双曲线上的点.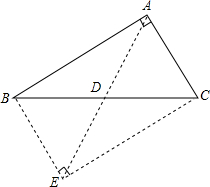 已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD.
已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD. 如图,A,B,C是同一直线上的三个点,图中共有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?
如图,A,B,C是同一直线上的三个点,图中共有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?