题目内容
10．化简（$\sqrt{3}$-2）2002•（$\sqrt{3}$+2）2003的结果为（ ）| A． | -1 | B． | $\sqrt{3}$-2 | C． | $\sqrt{3}$+2 | D． | -$\sqrt{3}$-2 |
分析 先根据同底数幂的乘法变形，再根据积的乘方的逆运算进行计算即可．
解答 解：原式=（$\sqrt{3}$-2）2002•（$\sqrt{3}$+2）2002•（$\sqrt{3}$+2）
=[（$\sqrt{3}$-2）•（$\sqrt{3}$+2）]2002•（$\sqrt{3}$+2）
=1×（$\sqrt{3}$+2）
=$\sqrt{3}$+2，
故选C．
点评 本题考查了二次根式的混合运算，熟练掌握积的乘方、同底数幂的乘法以及它们的逆运算是解题的关键．
练习册系列答案
相关题目
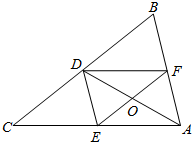已知：如图，在△ABC中，DE、DF是△ABC的中位线，连接EF、AD，其交点为O．求证：
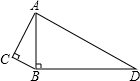如图，∠C=∠ABD=90°，AC=4，BC=3，BD=12，求AD的长．
5．下列分式一定有意义的是（ ）
| A． | $\frac{{x}^{2}+1}{{x}^{2}-1}$ | B． | $\frac{x+1}{{x}^{2}}$ | C． | $\frac{x-1}{{x}^{2}+1}$ | D． | $\frac{{x}^{2}}{x+1}$ |
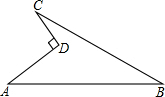如图所示的一块地，AD=9m，CD=12m，∠ADC=90°，AB=39m，BC=36m，求这块地的面积．
2．
已知OA，OB是⊙O的半径，点C在⊙O上，∠OBA=50°，则∠C的度数为（ ）
已知OA，OB是⊙O的半径，点C在⊙O上，∠OBA=50°，则∠C的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 80° |
已知：表示a、b两个实数的点在数轴上的位置如图所示，请你化简$|{a-b}|+\sqrt{{{（{a+b}）}^2}}$．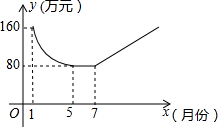
保护生态环境，建设绿色社会已经从理念变为人们的行动，某化工厂2011年1月的利润为160万元，设2011年1月为第1个月，第x个月的利润为y万元，由于排污超标，该厂决定从2011年1月底起适当限产，并投入资金进行治污改造，整个工程经过治污改造、调试、全面投产是三个时期，经测算：从1月到5月为治污改造期，y是x的二次函数，且其图象的顶点为（5，80），到5月底治污改造工程顺利完成，进接的6月、7月为调试期，月利润和5月份持平，调试期过后，设备全面投产，该厂每月利润比前一个月增加15万元，如图所示．