题目内容
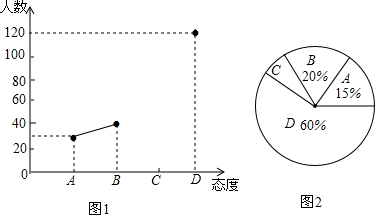
2．
已知OA，OB是⊙O的半径，点C在⊙O上，∠OBA=50°，则∠C的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 80° |
分析 根据三角形的内角和定理求得∠AOB的度数，再进一步根据圆周角定理求解．
解答 解：∵OA=OB，∠OBA=50°，
∴∠OAB=∠OBA=50°，
∴∠AOB=180°-50°×2=80°，
∴∠C$\frac{1}{2}$∠AOB=40°．
故选B．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
10．化简（$\sqrt{3}$-2）2002•（$\sqrt{3}$+2）2003的结果为（ ）
| A． | -1 | B． | $\sqrt{3}$-2 | C． | $\sqrt{3}$+2 | D． | -$\sqrt{3}$-2 |
17．下面的多项式中，能因式分解的是（ ）
| A． | m2+n2 | B． | m2+4m+1 | C． | m2-n | D． | m2-2m+1 |
11．下列变形中，从左向右是因式分解的是（ ）
| A． | x2-9+6x=（x+3）（x-3）+6x | B． | x2-8x+16=（x-4）2 | ||
| C． | （x-1）2=x2-2x+1 | D． | x2+1=x（x+$\frac{1}{x}$） |
12．
一种产品的进价为40元，某公司在销售这种产品时，每年总开支为100万元（不含进价）．经过若干年销售得知，年销售量y（万件）是销售单价x（元）的一次函数，并得到如下部分数据：
（1）求y关于x的函数关系式；
（2）写出该公司销售这种产品的年利润w（万元）关于销售单价x（元）的函数关系式；当销售单价x为何值时，年利润最大？
（3）试通过（2）中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围，使年利润不低于60万元．
一种产品的进价为40元，某公司在销售这种产品时，每年总开支为100万元（不含进价）．经过若干年销售得知，年销售量y（万件）是销售单价x（元）的一次函数，并得到如下部分数据：| 销售单价x（元） | 50 | 60 | 70 | 80 |
| 年销售量y（万件） | 5.5 | 5 | 4.5 | 4 |
（2）写出该公司销售这种产品的年利润w（万元）关于销售单价x（元）的函数关系式；当销售单价x为何值时，年利润最大？
（3）试通过（2）中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围，使年利润不低于60万元．