题目内容
18.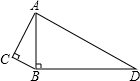 如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,求AD的长.
如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,求AD的长.
分析 先根据勾股定理求出AB,再根据勾股定理去除AD即可.
解答 解:在Rt△ACB中,由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
在Rt△ABD中,由勾股定理得:AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13.
点评 本题考查了勾股定理的应用,能运用勾股定理进行计算是解此题的关键,注意:直角三角形的两直角边的平方和等于斜边的平方.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
3.体育课上,某班两名同学分别进行了5次短跑训练,要判断哪一位同学的成绩比较稳定,通常要比较两名同学成绩的( )
| A. | 平均数 | B. | 方差 | C. | 众数 | D. | 中位数 |
4.在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球,从中任意摸出一个球,则摸出白球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
10.化简($\sqrt{3}$-2)2002•($\sqrt{3}$+2)2003的结果为( )
| A. | -1 | B. | $\sqrt{3}$-2 | C. | $\sqrt{3}$+2 | D. | -$\sqrt{3}$-2 |