题目内容
15.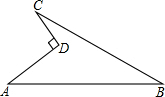 如图所示的一块地,AD=9m,CD=12m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积.
如图所示的一块地,AD=9m,CD=12m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积.
分析 连接AC,利用勾股定理求出AC,求出△ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
解答 解:解:连结AC,
由勾股定理可知
AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\sqrt{1{2}^{2}+{9}^{2}}$=15,
又∵AC2+BC2=152+362=392=AB2,
∴△ABC是直角三角形,
故这块地的面积=S△ABC-S△ACD=$\frac{1}{2}$×15×36-$\frac{1}{2}$×12×9=216(m)2,
即这块地的面积是216平方米.
点评 此题主要考查了直角三角形面积公式以及勾股定理以及逆定理的应用.关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
20.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | 5a-2a=3a | C. | a2•a3=a6 | D. | (a+b)2=a2+b2 |
10.化简($\sqrt{3}$-2)2002•($\sqrt{3}$+2)2003的结果为( )
| A. | -1 | B. | $\sqrt{3}$-2 | C. | $\sqrt{3}$+2 | D. | -$\sqrt{3}$-2 |
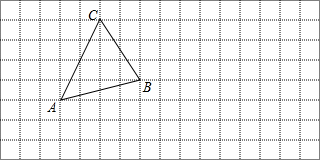
 已知三角形ABC、点D为点B平移后的对应点,过点D作三角形ABC平移后的图形.
已知三角形ABC、点D为点B平移后的对应点,过点D作三角形ABC平移后的图形.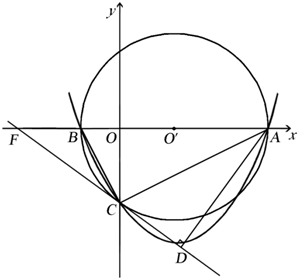 如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.