题目内容
2．在下列实数：$\frac{1}{3}$，$\sqrt{2}$，$-\sqrt{3}$，π，3.14中任取一个，取到有理数的概率为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
分析 用有理数的个数除以所有数的个数即可求得取到有理数的概率．
解答 解：实数$\frac{1}{3}$，$\sqrt{2}$，$-\sqrt{3}$，π，3.14中$\frac{1}{3}$和3.14是有理数，有理数的个数为2个，
则取到有理数的概率P=$\frac{2}{5}$，
故选B．
点评 本题考查了概率公式，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．
练习册系列答案
相关题目
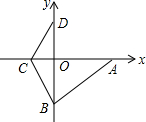如图，在平面直角坐标系中，A点的坐标为（a，0），B点的坐标为（0，b），a，b满足|$\frac{1}{2}$a-4|+$\sqrt{{b}^{2}-36}$=0，C在x轴负半轴上，且OC=$\frac{1}{2}$OB．
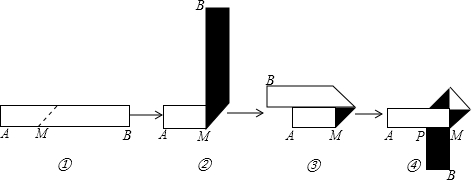
如图，已知AB∥CD∥EF，若AC：CE=2：3，BD=6，那么BF=15．
11．在函数y=$\frac{{\sqrt{x}}}{x-5}$中，自变量x的取值范围是（ ）
| A． | x≥0 | B． | x≥5且x≠0 | C． | x≥0且x≠5 | D． | x≥5 |