��Ŀ����
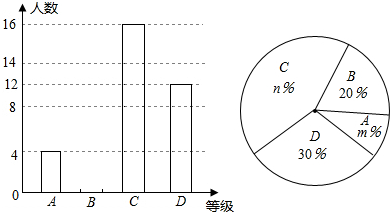
17�������У�����ϲ�������Ա����۳���ͼ�ܵ���״���۵�������ͼ����ͼ�ܵ�˳����ʾ����Ӱ���ֱ�ʾֽ���ķ��棩�����ͼ���е�ֽ����Ϊ26cm����Ϊxcm���ֱ�ش��������⣺���۲������۵��Ĺ��̣�����ͼ���еġ�AMB�Ķ���ӦΪ90�㣻
����Ϊ�˱�֤���۳�ͼ�ܵ���״����ֽ�����˾�������P��������x��ȡֵ��Χ��
�����������Ҫ�۳�ͼ�ܵ���״������Ϊ�����ۣ�ϣ��ֽ�����˳�����P�ij�����ȣ�������ͼ������Գ�ͼ�Σ������ڿ�ʼ�۵�ʱ���M���A�ľ��루��x��ʾ����
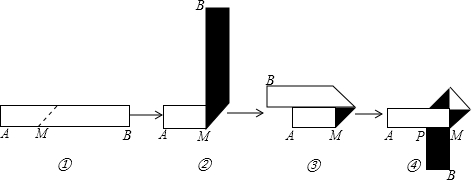
���� ��1�������۵��ķ�����֪��AMB�Ķ�����
��2����ͼ�з�ʽ�۵���ɵõ���ȥ���ˣ�ֽ��ʹ�õij���Ϊ5x����ôֽ��ʹ�õij���Ӧ����0��С��ֽ���ܳ��ȣ�
��3������ͼ������Գ�ͼ�Σ���ôAM=AP+PM=AP+ֽ����x��
��� �⣺��1�������۵��ķ�����֪��AMB=90�㣬
�ʴ�Ϊ��90�㣻
��2������ֽ���̿�֪0��5x��26��
��0��x��$\frac{26}{5}$��
��3����ͼ��Ϊ��Գ�ͼ�Σ�
��AM=AP+x=$\frac{26-5x}{2}$+x=13-$\frac{3}{2}$x��
����M���A�ľ����ǣ�13-$\frac{3}{2}$x��cm��
���� ���⿼��ѧ���Ķ��ֲ�����������֪�۵��������ǽ������Ĺؼ����ѵ��ǵõ�ֽ����ȥ����ʹ�õ�ֽ���ij��ȣ�

��ϰ��ϵ�д�
 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�
�����Ŀ
2��������ʵ����$\frac{1}{3}$��$\sqrt{2}$��$-\sqrt{3}$���У�3.14����ȡһ����ȡ���������ĸ���Ϊ��������
| A�� | $\frac{1}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{4}{5}$ |
9��Ҫʹ��ʽ$\frac{x+2}{x-1}$�����壬��x��ȡֵӦ���㣨������
| A�� | x��-2 | B�� | x��1 | C�� | x=-2 | D�� | x=1 |
7���������㣺��1��2x3-x2=x����2��x3•��x5��2=x13����3����-x��6�£�-x��3=x3����4����-2x3y��2=4x6y2��������ȷ���ǣ�������
| A�� | ��1����2�� | B�� | ��2����4�� | C�� | ��2����3�� | D�� | ��3����4�� |
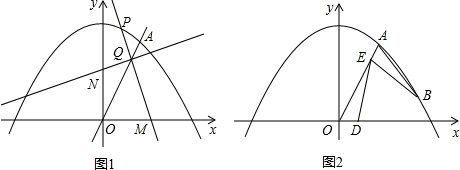
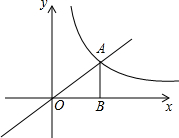 ��ͼ������������y=$\frac{k}{x}$��ͼ����һ�κ���y=mx��ͼ���ڵ�A��AB��ֱ��x�ᣬ����ΪB������AB=OB=2��
��ͼ������������y=$\frac{k}{x}$��ͼ����һ�κ���y=mx��ͼ���ڵ�A��AB��ֱ��x�ᣬ����ΪB������AB=OB=2��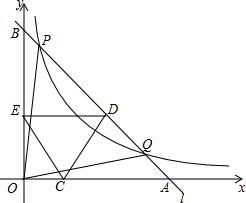 ��ͼ����֪˫����y=$\frac{k}{x}��x��0��$�뾭����A��1��0����B��0��1����ֱ�߽���P��Q���㣬��P�ĺ�������Q�������궼��$\frac{1}{4}$������OP��OQ��
��ͼ����֪˫����y=$\frac{k}{x}��x��0��$�뾭����A��1��0����B��0��1����ֱ�߽���P��Q���㣬��P�ĺ�������Q�������궼��$\frac{1}{4}$������OP��OQ��