题目内容
12.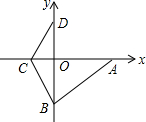 如图,在平面直角坐标系中,A点的坐标为(a,0),B点的坐标为(0,b),a,b满足|$\frac{1}{2}$a-4|+$\sqrt{{b}^{2}-36}$=0,C在x轴负半轴上,且OC=$\frac{1}{2}$OB.
如图,在平面直角坐标系中,A点的坐标为(a,0),B点的坐标为(0,b),a,b满足|$\frac{1}{2}$a-4|+$\sqrt{{b}^{2}-36}$=0,C在x轴负半轴上,且OC=$\frac{1}{2}$OB.(1)求直线BC的解析式;
(2)已知AB=10,求$\frac{∠ABO}{∠CBO.}$.
分析 (1)先根据非负数的性质求出a、b的值,故可得出A、B的坐标,由OC=$\frac{1}{2}$OB可得出点C的坐标,利用待定系数法求出直线BC的解析式即可;
(2)在线段OA上截取OC=OE,根据SAS定理可得出△OCB≌△OEB,故∠OBC=∠OBE,过点E作EF⊥AB于点F,根据三角形的面积公式求出EF的长,由角平分线的判定定理可知BE是∠ABO的平分线,由此可得出结论.
解答 解:(1)∵a,b满足|$\frac{1}{2}$a-4|+$\sqrt{{b}^{2}-36}$=0,
∴$\frac{1}{2}$a-4=0,b2-36=0,
解得a=8,b=6(舍去)或b=-6,
∴A(0,8),B(0,-6),
∴OA=8,OB=6.
∵OC=$\frac{1}{2}$OB,
∴B(-3,0),
设直线BC的解析式为y=kx+b(k≠0),
则$\left\{\begin{array}{l}-3k+b=0\\ b=-6\end{array}\right.$,
解得k=-2.
∴直线BC的解析式为y=-2x-6;
(2)如图,在线段OA上截取OC=OE=3,
在△OCB与△OEB中,
$\left\{\begin{array}{l}OC=OE\\∠BOC=∠BOE\\ OB=OB\end{array}\right.$,
∴△OCB≌△OEB(SAS),
∴∠OBC=∠OBE.
过点E作EF⊥AB于点F, ∵OA=8,OE=3,AB=10,
∵OA=8,OE=3,AB=10,
∴AE=5,
∴AE•OB=AB•EF,
∴EF$\frac{AE•OB}{AB}$=$\frac{5×6}{10}$=3,
∴EF=OE,
∴OE是∠ABO的平分线,
∴∠ABO=2∠OBE=2∠CBO,即$\frac{∠ABO}{∠CBO}$=2.
点评 本题考查的是一次函数综合题,涉及到待定系数法求一次函数的解析式、角平分线的判定与性质等知识,根据题意作出辅助线,构造出角平分线是解答此题的关键.

| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 D. x﹣5y=6
D. x﹣5y=6
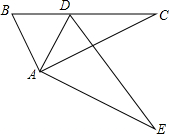 如图,Rt△ABC绕点直角顶点A旋转一定角度后得到△ADE,且点D落在BC上.
如图,Rt△ABC绕点直角顶点A旋转一定角度后得到△ADE,且点D落在BC上.