题目内容
13．三角形的一边长为2，它的对角为30°，则此三角形外接圆的半径为2．分析 作直径CD，连接BD，根据直径所对的圆周角是90°得到∠DBC=90°，根据圆周角定理得到∠D=∠A=30°，根据直角三角形中，30°所对的直角边是斜边的一半得到直径CD的长，得到答案．
解答 
解：作直径CD，连接BD，
∵CD为直径，
∴∠DBC=90°，又∠D=∠A=30°，
∴CD=2BC=4，
∴此三角形外接圆的半径为2，
故答案为：2．
点评 本题考查的是圆周角定理和直角三角形的性质，掌握同弧所对的圆周角相等、直径所对的圆周角是90°和直角三角形中，30°所对的直角边是斜边的一半是解题的关键．
练习册系列答案
相关题目
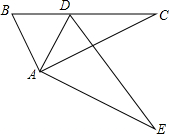如图，Rt△ABC绕点直角顶点A旋转一定角度后得到△ADE，且点D落在BC上．
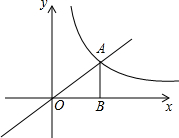如图，反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx的图象交于点A，AB垂直于x轴，垂足为B，并且AB=OB=2．
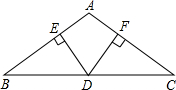在△ABC中，AB=AC，D是BC边上的点，DE⊥AB于E，DF⊥AC于F．
2．在下列实数：$\frac{1}{3}$，$\sqrt{2}$，$-\sqrt{3}$，π，3.14中任取一个，取到有理数的概率为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |