题目内容
11．
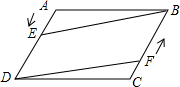如图，在?ABCD中，点E从A向D运动，点F从C向B运动，点E的运动速度m与点F的运动速度n满足m=n关系时，四边形BEDF为平行四边形．
分析 由平行四边形的性质得出AD∥BC且AD=BC，由m=n，得出AE=CF，因此DE=BF，即可得出四边形BEDF为平行四边形．
解答 解：点E的运动速度m与点F的运动速度n满足m=n时，四边形BEDF为平行四边形．理由如下：
∵四边形ABCD是平行四边形，
∴AD∥BC且AD=BC，
即DE∥BF，
∵m=n，
∴AE=CF，
∴DE=BF，
∴四边形BEDF为平行四边形．
故答案为：m=n．
点评 本题主要考查的是平行四边形的性质和判定；熟练掌握平行四边形的性质和判定定理是解题的关键．
练习册系列答案
相关题目
1．
如图，矩形ABCD的面积为16cm2，对交线交于点O；以AB、AO为邻边作平行四边AOC1B，对角线交于点O1，以AB、AO1为邻边作平行四边形AO1C2B，…；依此类推，则平行四边形AO4C5B的面积为（ ）
如图，矩形ABCD的面积为16cm2，对交线交于点O；以AB、AO为邻边作平行四边AOC1B，对角线交于点O1，以AB、AO1为邻边作平行四边形AO1C2B，…；依此类推，则平行四边形AO4C5B的面积为（ ）| A． | $\frac{1}{2}$cm2 | B． | 1cm2 | C． | 2cm2 | D． | 4cm2 |
2．在-5，0，π，$\sqrt{2}$这四个数中，最大的有理数的是（ ）
| A． | -5 | B． | 0 | C． | π | D． | $\sqrt{2}$ |
16．
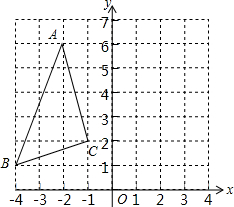如图，如果将△ABC先向右平移1个单位长度，再绕原点O顺时针旋转90°，得到△A1B1C1，那么点A的对应点A1的坐标为（ ）
如图，如果将△ABC先向右平移1个单位长度，再绕原点O顺时针旋转90°，得到△A1B1C1，那么点A的对应点A1的坐标为（ ）| A． | （1，3） | B． | （2，0） | C． | （6，1） | D． | （6，2） |
如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，求证：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形．