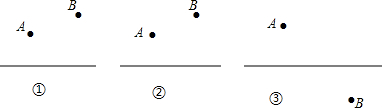题目内容
3.若多项式mx3+3nxy2-2x3-xy2+y中不含三次项,求2m+3n的值.分析 根据题意得出关于m,n的等式进而求出答案.
解答 解:∵多项式mx3+3nxy2-2x3-xy2+y中不含三次项,
∴$\left\{\begin{array}{l}{m-2=0}\\{3n-1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=2}\\{n=\frac{1}{3}}\end{array}\right.$,
故2m+3n=4+1=5.
点评 此题主要考查了多项式,正确把握多项式次数确定方法是解题关键.

练习册系列答案
相关题目
8.下列事件中,是不可能事件的是( )
| A. | 买一张电影票,座位号是偶数 | B. | 度量三角形的内角和,结果是360° | ||
| C. | 明天会下雨 | D. | 设计运动员射击一次,命中8环 |
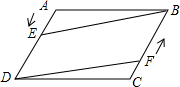 如图,在?ABCD中,点E从A向D运动,点F从C向B运动,点E的运动速度m与点F的运动速度n满足m=n关系时,四边形BEDF为平行四边形.
如图,在?ABCD中,点E从A向D运动,点F从C向B运动,点E的运动速度m与点F的运动速度n满足m=n关系时,四边形BEDF为平行四边形.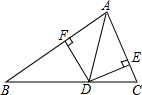 如图,点D是BC边上的点,DE⊥AB于E,DF⊥AC于F,AE=AF,连接AD,已知△ABD的面积为s1,△ACD的面积为s2,BC=a,AC=b,AB=c.
如图,点D是BC边上的点,DE⊥AB于E,DF⊥AC于F,AE=AF,连接AD,已知△ABD的面积为s1,△ACD的面积为s2,BC=a,AC=b,AB=c.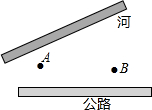 如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.
如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.