题目内容
已知抛物线y=ax2+4bx+1-3b和y=bx2+ax+3a-2b都经过纵坐标相同的两点A、B,分别交y轴于C、D两点,点C、D在原点的同侧,且OC:OD=1:4,ab<0,试确定这两条抛物线的解析式.
考点:待定系数法求二次函数解析式
专题:
分析:由于抛物线y=ax2+4bx+1-3b和y=bx2+ax+3a-2b都经过纵坐标相同的两点A、B,则它们的对称轴相同,以及根据OC:OD=1:4列出含a、b的方程组,解方程组求得a、b的值,即可求得这两条抛物线的解析式.
解答:解:∵ab<0,抛物线y=ax2+4bx+1-3b和y=bx2+ax+3a-2b都经过纵坐标相同的两点A、B,
∴它们的对称轴相同,
由题意得:
,解得
,
∴这两条抛物线的解析式:y=-2x2+4x-2和y=x2-2x+3a-8.
∴它们的对称轴相同,
由题意得:
|
|
∴这两条抛物线的解析式:y=-2x2+4x-2和y=x2-2x+3a-8.
点评:本题考查了待定系数法求二次函数的解析式,根据题目给定的条件,找出等量关系是解本题的关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
非负数a、b、c满足a+b-c=2,a-b+2c=1,则s=a+b+c的最大值与最小值的和为( )
| A、5 | B、9 | C、10 | D、12 |
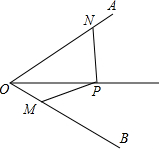 如图,已知点P在∠AOB的平分线上,且∠ONP+∠OMP=180°,求证:PM=PN.
如图,已知点P在∠AOB的平分线上,且∠ONP+∠OMP=180°,求证:PM=PN.