题目内容
非负数a、b、c满足a+b-c=2,a-b+2c=1,则s=a+b+c的最大值与最小值的和为( )
| A、5 | B、9 | C、10 | D、12 |
考点:一次函数的性质
专题:
分析:把c看作常数表示出a、b,再根据a、b、c都是非负数求出c的取值范围,然后表示出s,再根据一次函数的增减性求出最大值和最小值,然后相加计算即可得解.
解答:解:由题意得,a+b=c+2,a-b=1-2c,
解得
,
∵a、b为非负数,
∴
(3-c)≥0,
(1+3c)≥0,
解得-
≤c≤3,
∵c也是非负数,
∴0≤c≤3,
∵s=a+b+c=
(3-c)+
(1+3c)+c=2c+2,
∴当c=3时,s最大=2×3+2=8,
当c=0时,s最小=2×0+2=2,
所以,最大值与最小值的和=8+2=10.
故选C.
解得
|
∵a、b为非负数,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得-
| 1 |
| 3 |
∵c也是非负数,
∴0≤c≤3,
∵s=a+b+c=
| 1 |
| 2 |
| 1 |
| 2 |
∴当c=3时,s最大=2×3+2=8,
当c=0时,s最小=2×0+2=2,
所以,最大值与最小值的和=8+2=10.
故选C.
点评:本题考查了一次函数的性质,解二元一次方程组,解一元一次不等式组,难点在于考虑利用一次函数的性质解答.

练习册系列答案
相关题目
若x=-1,式子
与
的值相等,则m的值是( )
| 3x+m-1 |
| 4 |
| 2x-m+1 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
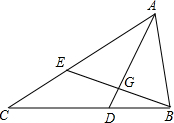 在△ABC中,AB<BC<CA,且AC-AB=2,D点在边BC上,且AD平分∠BAC.E为边AC上的一点,连接BE交AD于点G,且
在△ABC中,AB<BC<CA,且AC-AB=2,D点在边BC上,且AD平分∠BAC.E为边AC上的一点,连接BE交AD于点G,且
 半径为R的⊙O1和半径为r的⊙O2外切于点P,AB为两圆的外公切线,切点为A、B,连心线O2O1交圆⊙O1于C,交⊙O2于D,CA与DB的延长线相交于Q.若R=3r,求∠ABQ的度数.
半径为R的⊙O1和半径为r的⊙O2外切于点P,AB为两圆的外公切线,切点为A、B,连心线O2O1交圆⊙O1于C,交⊙O2于D,CA与DB的延长线相交于Q.若R=3r,求∠ABQ的度数.