题目内容
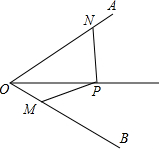 如图,已知点P在∠AOB的平分线上,且∠ONP+∠OMP=180°,求证:PM=PN.
如图,已知点P在∠AOB的平分线上,且∠ONP+∠OMP=180°,求证:PM=PN.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:根据补角的性质,可得∠ONP=∠PME,根据角平分线的性质,可得PD与PE的关系,根据全等三角形的判定与性质,可得答案.
解答:证明:过点p作PD⊥OA,PE⊥OB, ,
,
∴∠NDP=∠MEP=90°
∵∠OMP+∠ONP=180°,∠OMP+∠PME=180°
∴∠ONP=∠PME.
∵OP平分∠AOB,PD⊥OA,PE⊥OB,
∴PD=PE.
在△PDN和△PEM中
,
∴△PDN≌△PEM(AAS),
∴PN=PM.
 ,
,∴∠NDP=∠MEP=90°
∵∠OMP+∠ONP=180°,∠OMP+∠PME=180°
∴∠ONP=∠PME.
∵OP平分∠AOB,PD⊥OA,PE⊥OB,
∴PD=PE.
在△PDN和△PEM中
|
∴△PDN≌△PEM(AAS),
∴PN=PM.
点评:本题考查了全等三角形的判定与性质,利用了补角的性质,角平分线的性质,全等三角形的判定与性质.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
若x=-1,式子
与
的值相等,则m的值是( )
| 3x+m-1 |
| 4 |
| 2x-m+1 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
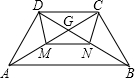 如图,在梯形ABCD中,AB∥CD,并且AB=2CD,M、N分别是对角线AC,BD的中点,设梯形ABCD的周长为L1,四边形CDMN的周长为L2,求L1:L2.
如图,在梯形ABCD中,AB∥CD,并且AB=2CD,M、N分别是对角线AC,BD的中点,设梯形ABCD的周长为L1,四边形CDMN的周长为L2,求L1:L2. 半径为R的⊙O1和半径为r的⊙O2外切于点P,AB为两圆的外公切线,切点为A、B,连心线O2O1交圆⊙O1于C,交⊙O2于D,CA与DB的延长线相交于Q.若R=3r,求∠ABQ的度数.
半径为R的⊙O1和半径为r的⊙O2外切于点P,AB为两圆的外公切线,切点为A、B,连心线O2O1交圆⊙O1于C,交⊙O2于D,CA与DB的延长线相交于Q.若R=3r,求∠ABQ的度数.