题目内容
18．下列命题是假命题的是（ ）| A． | 平行四边形的对角相等 | B． | 四条边都相等的四边形是菱形 | ||
| C． | 正方形的两条对角线互相垂直 | D． | 矩形的两条对角线互相垂直 |
分析 利于平行四边形的性质、菱形的判定定理、正方形的性质及矩形的性质分别判断后即可确定正确的选项．
解答 解：A、平行四边形的对角相等，正确，为真命题；
B、四条边都相等的四边形是菱形，正确，是真命题；
C、正方形的两条对角线互相垂直，正确，为真命题；
D、矩形的两条对角线相等但不一定垂直，故错误，为假命题，
故选D．
点评 本题考查了命题与定理的知识，解题的关键是了解平行四边形的性质、菱形的判定定理、正方形的性质及矩形的性质，难度不大．
练习册系列答案
相关题目
9．要判断命题“若a＞b，则a2＞b2”是假命题，可举得反例是（ ）
| A． | a=1，b=-2 | B． | a=1，b=0 | C． | a=2，b=1 | D． | a=2，b=-1 |
在平面直角坐标系xOy中，一次函数的图象经过点A（2，3）与点B（0，5）．
如图，在平面直角坐标系中，菱形OBCD的顶点O、D的坐标分别是（0、0）、（3、4），求顶点C的坐标．
9．
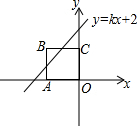如图，在平面直角坐标系中，四边形OABC是边长为1的正方形，顶点A、C分别在x轴的负半轴、y轴的正半轴上．若直线y=kx+2与边AB有公共点，则k的值可能为（ ）
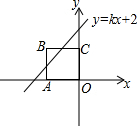如图，在平面直角坐标系中，四边形OABC是边长为1的正方形，顶点A、C分别在x轴的负半轴、y轴的正半轴上．若直线y=kx+2与边AB有公共点，则k的值可能为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | 3 |
10．
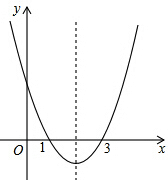已知二次函数y=ax2+bx+c的图象如图所示，则下列叙述正确的是（ ）
已知二次函数y=ax2+bx+c的图象如图所示，则下列叙述正确的是（ ）| A． | abc＜0 | B． | -3a+c＜0 | C． | b2-4ac≥0 | D． | 5a+2b+c＞0 |