题目内容
4.如果方程$\frac{x-4}{3}$-8=-$\frac{x+2}{2}$的解与方程4x-(3a+1)=6x+2a-1的解相同,求式子a-a2的值.分析 先求得方程方程$\frac{x-4}{3}$-8=-$\frac{x+2}{2}$的解,然后将所求的x的值代入方程4x-(3a+1)=6x+2a-1求得a的值,最后在求代数式的值即可.
解答 解:$\frac{x-4}{3}$-8=-$\frac{x+2}{2}$
去分母得:2(x-4)-48=-3(x+2)
去括号得:2x-8-48=-3x-6,
移项得:2x+3x=-6+8+48,
合并同类项得:5x=50,
系数化为1得:x=10.
将x=10代入方程4x-(3a+1)=6x+2a-1得:40-(3a+1)=60+2a-1,
去括号得:40-3a-1=60+2a-1,
移项得:-3a-2a=60-1-40+1,
合并同类项得:-5a=20,
系数化为1得:a=-4.
a-a2=-4-(-4)2=-4-16=-20.
点评 本题主要考查的是同解方程的定义、解一元一次方程、求代数式的值,求得a的值是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
9.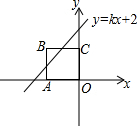 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
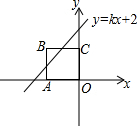 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
 如图,在正方形ABCD中,以CD为边向外作等边三角形CDE,连结AE、BE,则∠AEB=30°.
如图,在正方形ABCD中,以CD为边向外作等边三角形CDE,连结AE、BE,则∠AEB=30°. 如图,在平面直角坐标系中,菱形OBCD的顶点O、D的坐标分别是(0、0)、(3、4),求顶点C的坐标.
如图,在平面直角坐标系中,菱形OBCD的顶点O、D的坐标分别是(0、0)、(3、4),求顶点C的坐标.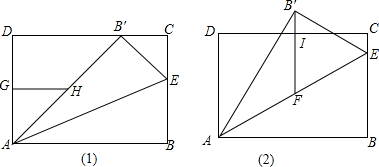
 如图,矩形ABCD的对角线相交于点O,BD=6,AD=3$\sqrt{3}$,则∠AOD=120度.
如图,矩形ABCD的对角线相交于点O,BD=6,AD=3$\sqrt{3}$,则∠AOD=120度.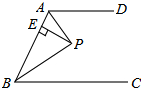 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=3,则两平行线AD与BC间的距离为( )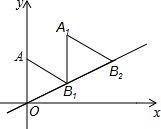 如图放置的△OAB1,△B1A1B2都是边长为2的等边三角形,边AO在y轴上,点B1,B2都在直线y=$\frac{\sqrt{3}}{3}$x上,则点B2的坐标为(2$\sqrt{3}$,2).
如图放置的△OAB1,△B1A1B2都是边长为2的等边三角形,边AO在y轴上,点B1,B2都在直线y=$\frac{\sqrt{3}}{3}$x上,则点B2的坐标为(2$\sqrt{3}$,2).