题目内容
12. 如图,已知正方形A1B1C1D1的面积为1,把它的各边延长一倍得到新的正方形A2B2C2D2,再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3,以此下去…,则正方形A9B9C9D9的周长是2500.
如图,已知正方形A1B1C1D1的面积为1,把它的各边延长一倍得到新的正方形A2B2C2D2,再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3,以此下去…,则正方形A9B9C9D9的周长是2500.
分析 由条件可得A1B2和A1A2,在Rt△A1A2B2中,利用勾股定理可求A2B2,同理可求得A3B3,从而可找出规律,可求得答案.
解答 解:
由题意可知A1B1=1,
∴A1B2=A2D1=2,
∴A1A2=1,
在Rt△A1A2B2中,由勾股定理可得A2B2=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
同理A3B3=$\sqrt{(\sqrt{5})^{2}+(2\sqrt{5})^{2}}$=5=($\sqrt{5}$)2,A4B4=($\sqrt{5}$)3,
∴A9B9=($\sqrt{5}$)8=625,
∴正方形A9B9C9D9的周长是2500,
故答案为:2500.
点评 本题主要考查勾股定理及正方形周长的计算,正确的找出规律是解题的关键,注意勾股定理的灵活运用.

练习册系列答案
相关题目
20. 如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
 如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )| A. | 4对 | B. | 1对 | C. | 2对 | D. | 3对 |
2. 如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
 如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )| A. | $\frac{25}{4}$π | B. | $\frac{25}{8}π$ | C. | $\frac{25}{16}π$ | D. | $\frac{25}{32}π$ |
 在△ABC中,已知∠C=90°,AC=6,BC=8.
在△ABC中,已知∠C=90°,AC=6,BC=8.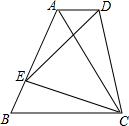 如图,四边形ABCD中,AD∥BC,AD<BC,AB=AC,点E在AB上,连接DE、DC、EC,∠DCE=∠ACB.
如图,四边形ABCD中,AD∥BC,AD<BC,AB=AC,点E在AB上,连接DE、DC、EC,∠DCE=∠ACB.