题目内容
17.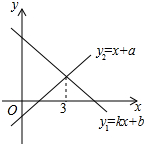 一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k>0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k>0;②a>0;③当x<3时,y1<y2中,正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据一次函数y1=kx+b与y2=x+a的图象在坐标平面内的位置关系确定k,b,a的取值范围,从而求解.
解答 解:由一次函数y1=kx+b的图象经过第一、二、四象限,
又由k<0时,直线必经过二、四象限,故知k<0,①错误.
再由图象过一、二象限,即直线与y轴正半轴相交,所以b>0.
由一次函数y2=x+a的图象经过第一、三、四象限,
再由图象过三、四象限,即直线与y轴负半轴相交,所以a<0,②错误.
当x>3时,一次函数y1=kx+b在y2=x+a的图象的下方,故y1<y2,错误.
故选A
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
8.关于x的一元二次方程(a+1)x2-4x+1=0有两个不相等的实数根,则a的取值范围是( )
| A. | a>3 | B. | a<3且a≠-1 | C. | a<3 | D. | a≥3且a≠-1 |
2. 如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
 如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )| A. | $\frac{25}{4}$π | B. | $\frac{25}{8}π$ | C. | $\frac{25}{16}π$ | D. | $\frac{25}{32}π$ |
2.股民李金上星期六买进某公司的股票,每股27元,如表为本周内该股票的涨跌情况
星期三收盘时.每股是26元;本周内最高价是每股27.5元;最低价是每股24.5元.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 |
| 每股涨跌 (与前一天相比) | -1.5 | -1 | +1.5 | +0.5 | +1 | -0.5 |
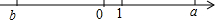 数轴上有b,0,1,a的四个数,如图所示,已知|a|=|b|,化简:|b+1|+|$\frac{a}{b}$|-|a+b|.
数轴上有b,0,1,a的四个数,如图所示,已知|a|=|b|,化简:|b+1|+|$\frac{a}{b}$|-|a+b|.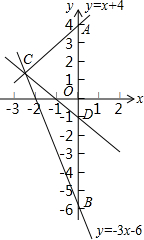 如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.
如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.