题目内容
1. 如图,玲玲在某公路的北侧沿AB行走,小梅在该公路的商侧沿CD行走,且AB∥CD.当小梅走到点E处时,发现玲玲在点M处,该时刻玲玲在小梅北偏东60°的方向上,随后她们继续沿各自的路线同时行走,当小梅行走36m到达点F处时,玲玲行走到与点M相距30m的点N处,此时玲玲在小梅北偏东45°的方向上.求该公路的宽度.(结果精确到0.1m.参考数据:$\sqrt{3}$≈1.73)
如图,玲玲在某公路的北侧沿AB行走,小梅在该公路的商侧沿CD行走,且AB∥CD.当小梅走到点E处时,发现玲玲在点M处,该时刻玲玲在小梅北偏东60°的方向上,随后她们继续沿各自的路线同时行走,当小梅行走36m到达点F处时,玲玲行走到与点M相距30m的点N处,此时玲玲在小梅北偏东45°的方向上.求该公路的宽度.(结果精确到0.1m.参考数据:$\sqrt{3}$≈1.73)
分析 作EH⊥AB于H,FG⊥AB于G,设宽为xm,根据方向角和锐角三角函数的定义表示出GN、HM,根据题意列出关系式求出x的值即可.
解答 解:作EH⊥AB于H,FG⊥AB于G,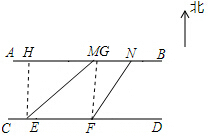
设宽为xm,
由题意得,HG=EF=36m,∠GFN=45°,∠HEM=30°,
∴GN=xm,HM=xtan60°=$\sqrt{3}$x,
则$\sqrt{3}$x+30=36+x,
解得x=$\frac{6}{\sqrt{3}-1}$=3($\sqrt{3}$+1)≈8.2m.
答:该公路的宽度是8.2m.
点评 本题考查的是解直角三角形的应用-方向角问题,正确作出辅助线、标注方向角、熟记锐角三角函数的定义是解题的关键,注意数形结合思想的应用.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
13.有下列结论:①sin230°+cos230°=sin260°;②sin45°=cos45°;③tan25°•tan65°=1;④若∠A为锐角,且sinA=cos28°,则∠A=62°.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.已知两边及其中一边的对角作三角形,下列结论正确的是( )
| A. | 有唯一一个三角形 | B. | 不能作出三角形 | ||
| C. | 有两个三角形 | D. | 以上三种情况都有可能 |

 如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.
如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.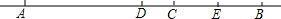 如图.已知A、B、C、D、E五点在同一直线上,D点是线段AB的中点,点E是线段BC的中点,若线段AC=12,则线段DE等于( )
如图.已知A、B、C、D、E五点在同一直线上,D点是线段AB的中点,点E是线段BC的中点,若线段AC=12,则线段DE等于( ) 萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题: