题目内容
13.已知一次函数y=$\frac{1}{2}x-3$的图象是直线l1,l1与y轴相交于点A,与x轴相交于点B,直线l2经过点B,并且与y轴相交于点C,点C到原点的距离是6个单位长度.(1)求直线l2所对应的一次函数表达式;
(2)求△ABC的面积.
分析 (1)先求出点A、B的坐标,然后分点C在y轴正半轴与负半轴两种情况写出点C的坐标,再利用待定系数法求直线解析式即可.
(2)根据C的坐标求△ABC的面积即可.
解答 解:(1)令x=0,则y=$\frac{1}{2}$×0-3=-3,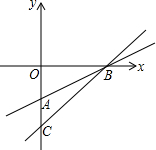
令y=0,则$\frac{1}{2}$x-3=0,解得x=6,
所以,点A(0,-3),B(6,0),
∵y轴上的点C到原点的距离是6个单位,
∴点C的坐标为(0,6),(0,-6),
设直线L2的解析式为y=kx+b,
则$\left\{\begin{array}{l}{6k+b=0}\\{b=6}\end{array}\right.$或$\left\{\begin{array}{l}{6k+b=0}\\{b=-6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$或$\left\{\begin{array}{l}{k=1}\\{b=-6}\end{array}\right.$,
所以直线L2所对应的一次函数关系式为y=-x+6或y=x-6;
(2)点C的坐标为(0,6)时,AC=9,
△ABC的面积=$\frac{1}{2}$×9×6=27,
点C的坐标为(0,-6)时,AC=3,
△ABC的面积=$\frac{1}{2}$×3×6=9.
故△ABC的面积为27或9.
点评 本题主要考查了两直线相交的问题,待定系数法求直线解析式,难点在于要分点C在y轴正半轴与负半轴两种情况讨论.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
18.抛物线y=x2-2x-1与x轴交点的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不能确定 |
5.下列各题的两个单项式为同类项的是( )
| A. | -$\frac{1}{2}$x2y与xy2 | B. | 3x2y与-4x2yz | C. | -3xy3与zy3 | D. | x2y与-3yx2 |
2.已知线段AB=3cm,反向延长线段AB到C,使BC=$\frac{5}{3}$AC,D是BC的中点,则线段AD的长为( )
| A. | $\frac{5}{2}$cm | B. | $\frac{5}{4}$cm | C. | $\frac{3}{2}$cm | D. | $\frac{1}{4}$cm |

 如图,玲玲在某公路的北侧沿AB行走,小梅在该公路的商侧沿CD行走,且AB∥CD.当小梅走到点E处时,发现玲玲在点M处,该时刻玲玲在小梅北偏东60°的方向上,随后她们继续沿各自的路线同时行走,当小梅行走36m到达点F处时,玲玲行走到与点M相距30m的点N处,此时玲玲在小梅北偏东45°的方向上.求该公路的宽度.(结果精确到0.1m.参考数据:$\sqrt{3}$≈1.73)
如图,玲玲在某公路的北侧沿AB行走,小梅在该公路的商侧沿CD行走,且AB∥CD.当小梅走到点E处时,发现玲玲在点M处,该时刻玲玲在小梅北偏东60°的方向上,随后她们继续沿各自的路线同时行走,当小梅行走36m到达点F处时,玲玲行走到与点M相距30m的点N处,此时玲玲在小梅北偏东45°的方向上.求该公路的宽度.(结果精确到0.1m.参考数据:$\sqrt{3}$≈1.73)