Question

16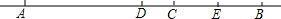．如图．已知A、B、C、D、E五点在同一直线上，D点是线段AB的中点，点E是线段BC的中点，若线段AC=12，则线段DE等于（　　）

• A． 10
• B． 8
• C． 6
• D． 4

Answer 1

分析 首先根据D点是线段AB的中点，点E是线段BC的中点，可得AD=BD，BE=CE；然后根据线段AC=12，可得BD+CD=12，据此求出CE+CD=6，即可判断出线段DE等于6．

解答 解：∵D点是线段AB的中点，
∴AD=BD，
∵点E是线段BC的中点，
∴BE=CE，
∵AC=12，
∴AD+CD=12，
∴BD+CD=12，
又∵BD=2CE+CD，
∴2CE+CD+CD=12，
即2（CE+CD）=12，
∴CE+CD=6，
即线段DE等于6．
故选：C．

点评 此题主要考查了两点间的距离的求法，要熟练掌握，解答此题的关键是要明确线段的中点的性质，并能推得AD=BD，BE=CE．