题目内容
9.边长为a的正六边形的面积为( )| A. | $\frac{3\sqrt{3}}{2}$a2 | B. | 6a2 | C. | $\frac{\sqrt{3}}{4}$a2 | D. | 3$\sqrt{3}$a2 |
分析 边长为a的正六边形的面积是边长是a的等边三角形的面积的6倍,据此即可求解.
解答 解:边长为a的等边三角形的面积是:$\frac{\sqrt{3}}{4}$a2,
则边长为a的正六边形的面积等于6×$\frac{\sqrt{3}}{4}$a2=$\frac{3\sqrt{3}}{2}$a2.
故选A.
点评 本题考查了正多边形和圆,熟知正六边形的半径把正六边形分成六个全等的等边三角形是解答此题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
18. 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )| A. | 从图中可以直接看出喜欢各种球类的具体人数 | |
| B. | 从图中可以直接看出全班的总人数 | |
| C. | 从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况 | |
| D. | 从图中可以直接看出全班同学现在喜欢各种球类人数的大小关系 |
19.若甲数为x,乙数为y,则“甲数的3倍比乙数的一半少2”,列成方程是( )
| A. | 3x$+\frac{1}{2}$y=2 | B. | $\frac{1}{2}y-3x$=2 | C. | 3x$-\frac{1}{2}y$=2 | D. | $\frac{1}{2}y$+2=3x |
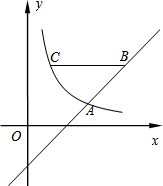 如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A. 如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)
如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可) 如图,在四边形ABCD中,AD∥BC,AB=AC,BE=CE=AD.
如图,在四边形ABCD中,AD∥BC,AB=AC,BE=CE=AD.