题目内容
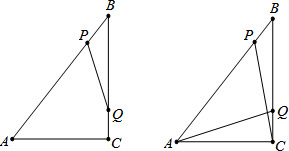
6. 已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.(1)求证:AD=EC;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
分析 (1)利用SAS证得△ACD≌△ECD后即可证得AD=EC;
(2)当点D是BC中点时,四边形ADCE是矩形;首先证得四边形ADCE是平行四边形,然后证得AD⊥BC即可利用有一个角是直角的平行四边形是矩形判定矩形.
解答 解:(1)由平移可得AB∥DE,AB=DE;
∴∠B=∠EDC,
∵AB=AC,
∴∠B=∠ACD,AC=DE,
∴∠EDC=∠ACD,
∵DC=CD,
∴△ACD≌△ECD(SAS),
∴AD=EC;
(2)当点D是BC中点时,四边形ADCE是矩形.
理由如下:∵AB=AC,点D是BC中点,
∴BD=DC,AD⊥BC,
由平移性质可知 四边形ABDE是平行四边形,
∴AE=BD,AE∥BD,
∴AE=DC,AE∥DC,
∴四边形ADCE是平行四边形,
∵AD⊥BC,
∴四边形ADCE是矩形.
点评 本题考查了矩形的判定,平行四边形的性质及全等三角形的判定与性质,能够正确的结合图形理解题意是解答本题的关键,难度不大.

练习册系列答案
相关题目
18. 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )| A. | 从图中可以直接看出喜欢各种球类的具体人数 | |
| B. | 从图中可以直接看出全班的总人数 | |
| C. | 从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况 | |
| D. | 从图中可以直接看出全班同学现在喜欢各种球类人数的大小关系 |
 如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)
如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)
 如果按图中虚线对折可以做成一个上底面为无盖的盒子,那么该盒子的下底面的字母是B.
如果按图中虚线对折可以做成一个上底面为无盖的盒子,那么该盒子的下底面的字母是B.