题目内容
12.计算:(1)($\sqrt{3}$)2-20+|-$\frac{1}{2}$|
(2)($\sqrt{54}$-$\sqrt{6}$)×$\sqrt{24}$
(3)2$\sqrt{12}$-3$\sqrt{48}$+$\sqrt{50}$;
(4)(7+4$\sqrt{3}$)(2-$\sqrt{3}$)2+(2+$\sqrt{3}$)(2-$\sqrt{3}$)
分析 (1)根据二次根式的性质即可求值.
(2)先将各二次根式化简,然后合并同类二次根式即可求值
(3)化为最简二次根式后进行合并同类二次根式即可求值
(4)先将7+4$\sqrt{3}$进行分解,然后提取公因式,最后再化简求值.
解答 解:(1)原式=3-1+$\frac{1}{2}$=$\frac{5}{2}$
(2)原式=(3$\sqrt{6}$-$\sqrt{6}$)×$\sqrt{24}$=24
(3)原式=4$\sqrt{3}$-12$\sqrt{3}$+5$\sqrt{2}$=-8$\sqrt{3}$+5$\sqrt{2}$
(4)原式=(2+$\sqrt{3}$)2(2-$\sqrt{3}$)2+(2+$\sqrt{3}$)(2-$\sqrt{3}$)
=1+1
=2
点评 本题考查二次根式的混合运算,解题的关键熟练二次根式的运算法则,本题属于基础题型.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
13. 有一实物模型如图所示,它的主视图是( )
有一实物模型如图所示,它的主视图是( )
 有一实物模型如图所示,它的主视图是( )
有一实物模型如图所示,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 已知∠AOB,利用尺规,求作∠A′O′B′,使得∠A′O′B′=∠AOB(保留作图痕迹).
已知∠AOB,利用尺规,求作∠A′O′B′,使得∠A′O′B′=∠AOB(保留作图痕迹). 如图,在平行四边形ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.求证:∠D=∠F.
如图,在平行四边形ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.求证:∠D=∠F.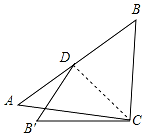 如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=48°,则∠ACB′=6°.
如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=48°,则∠ACB′=6°. 如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$
如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$