题目内容
4. 如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$
如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$(1)作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)所作的圆中,圆心角∠BOC=90°,圆的半径为1,劣弧$\widehat{BC}$的长为$\frac{1}{2}$π.
分析 (1)先作出AC的垂直平分线,交AB于点O,则点O即为圆心,最后作出△ABC的外接圆即可;
(2)根据圆周角定理即可得到∠BOC的度数,根据Rt△AOC即可得出AO的长,根据∠BOC=90°,BO=1,运用公式即可得到劣弧$\widehat{BC}$的长.
解答 解:(1)如图所示,⊙O即为所求;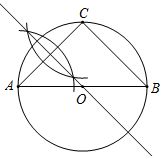
(2)如图所示,∠BOC=2∠A=90°,
Rt△AOC中,AO=AC×cos∠A=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1,即圆的半径为1,
$\widehat{BC}$=$\frac{90×π×1}{180}$=$\frac{1}{2}$π.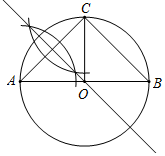
故答案为:90,1,$\frac{1}{2}$π.
点评 本题主要考查了复杂作图,解题时需要运用等腰直角三角形的性质以及弧长计算公式,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目

 小梅用两张同样大小的长方形硬纸片拼接成一个面积为900cm2的正方形,如图所示,按要求完成下列各小题.
小梅用两张同样大小的长方形硬纸片拼接成一个面积为900cm2的正方形,如图所示,按要求完成下列各小题. 如图,AB是⊙O的直径,点C在⊙O上,OD∥AC,交BC于D.若BD=1,则BC的长为2.
如图,AB是⊙O的直径,点C在⊙O上,OD∥AC,交BC于D.若BD=1,则BC的长为2.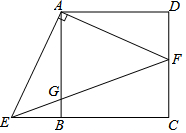 如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.
如图,在正方形ABCD中,F是CD边上的一点,AE⊥AF,AE交CB的延长线于点E,连接EF交AB于点G.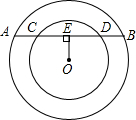 已知:如图,在两个同心圆中,大圆的弦AB与小圆相交于点C、D,且AC=CD,DE⊥AB,垂足为点E,求证:BC=4ED.
已知:如图,在两个同心圆中,大圆的弦AB与小圆相交于点C、D,且AC=CD,DE⊥AB,垂足为点E,求证:BC=4ED.