题目内容
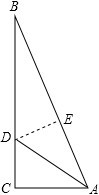 有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求△DEB的面积.
有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求△DEB的面积.考点:翻折变换(折叠问题)
专题:
分析:借助翻转变换的性质求出线段BE的长度;运用勾股定理求出DE的长度问题即可解决.
解答: 解:由勾股定理得:
解:由勾股定理得:
AB2=AC2+BC2,
∴AB=
=50(cm);
由题意得:
∠AED=∠C=90°,DE=DC(设为x),AE=AC=30cm,
∴BE=50-30=20(cm),BD=(40-x)cm;
由勾股定理得:
(40-x)2=x2+202,
解得:x=15(cm),
∴S△DEB=
BE•DE=
×20×15=150(cm2),
即△DEB的面积为150cm2.
 解:由勾股定理得:
解:由勾股定理得:AB2=AC2+BC2,
∴AB=
| 302+402 |
由题意得:
∠AED=∠C=90°,DE=DC(设为x),AE=AC=30cm,
∴BE=50-30=20(cm),BD=(40-x)cm;
由勾股定理得:
(40-x)2=x2+202,
解得:x=15(cm),
∴S△DEB=
| 1 |
| 2 |
| 1 |
| 2 |
即△DEB的面积为150cm2.
点评:该命题主要考查了翻折变换及其应用问题;解题的关键是灵活运用翻折变换的性质求出图中有关的边或角;运用勾股定理求出有关线段的长度;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
下列说法中,正确的是( )
A、单项式
| ||||
| B、-3x2y+4x-1是三次三项式,常数项是1 | ||||
| C、单项式a的系数是0,次数是0 | ||||
D、单项式-
|
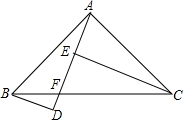 如图,△ABC中,∠BAC=90°,AB=AC,F是BC上一点,BD⊥AF交AF的延长线于D,CE⊥AF于E,已知CE=5,BD=2,则ED=
如图,△ABC中,∠BAC=90°,AB=AC,F是BC上一点,BD⊥AF交AF的延长线于D,CE⊥AF于E,已知CE=5,BD=2,则ED=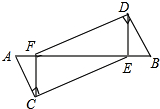 如图,已知A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.
如图,已知A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.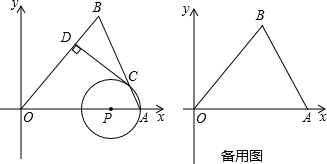
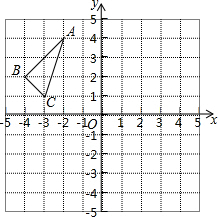 △ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.