题目内容
一个正多边形的内角和是1440°,则此多边形的边数是 ,对角线共有 条.
考点:多边形内角与外角
专题:
分析:设这个多边形的边数为n,根据多边形内角和公式可得:(n-2)×180=1440,再解方程可得n的值;然后再根据n边形从一个顶点出发可引出(n-3)条对角线.从n个顶点出发引出(n-3)条,而每条重复一次,所以n边形对角线的总条数为:
(n≥3,且n为整数)可得答案.
| n(n-3) |
| 2 |
解答:解:设这个多边形的边数为n,由题意得:(n-2)×180=1440,
解得:n=10,
过其中一个顶点可以作对角线条数:10-3=7,
这个多边形对角线总条数:
=35,
故答案为:10;35.
解得:n=10,
过其中一个顶点可以作对角线条数:10-3=7,
这个多边形对角线总条数:
| 10(10-3) |
| 2 |
故答案为:10;35.
点评:此题主要考查了多边形内角和公式,以及对角线,关键是掌握多边形内角和定理:(n-2)•180°(n≥3)且n为整数).

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
下列说法正确的是( )
| A、0不是单项式 | ||
| B、x没有系数 | ||
C、
| ||
| D、-xy是单项式 |
下列计算正确的是( )
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(-
|
数-5与-4的和比它们的绝对值的和( )
| A、大9 | B、小9 | C、小18 | D、相等 |
 如图,某学校要在校园内墙边的空地上修建一个长方形的存车处,存车处的一面靠墙(墙长22m),另外三面用90m长的铁栅栏围起来,如果这个存车处的面积为700m2,求这个长方形存车处的长和宽.
如图,某学校要在校园内墙边的空地上修建一个长方形的存车处,存车处的一面靠墙(墙长22m),另外三面用90m长的铁栅栏围起来,如果这个存车处的面积为700m2,求这个长方形存车处的长和宽.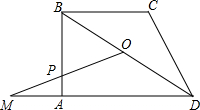 如图,梯形ABCD中,AD∥BC,∠A=90°,BC=CD,点O是对角线BD的中点,BD=5,tan∠DBC=
如图,梯形ABCD中,AD∥BC,∠A=90°,BC=CD,点O是对角线BD的中点,BD=5,tan∠DBC=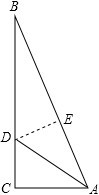 有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求△DEB的面积.
有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求△DEB的面积.