题目内容
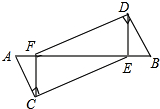 如图,已知A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.
如图,已知A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.求证:△ACF≌△BDE.
考点:全等三角形的判定与性质
专题:证明题
分析:先由条件证明Rt△ACE≌Rt△BDF,得到∠A=∠B,再证明△ACF≌△BDE即可
解答:证明:∵AC⊥CE,BD⊥DF(已知),
∴∠ACE=∠BDF=90°(垂直的定义),
在Rt△ACE和Rt△BDF中,
,
∴Rt△ACE≌Rt△BDF(HL),
∴∠A=∠B(全等三角形的对应角相等),
∵AE=BF(已知),
∴AE-EF=BF-EF(等式性质),
即AF=BE,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(SAS).
∴∠ACE=∠BDF=90°(垂直的定义),
在Rt△ACE和Rt△BDF中,
|
∴Rt△ACE≌Rt△BDF(HL),
∴∠A=∠B(全等三角形的对应角相等),
∵AE=BF(已知),
∴AE-EF=BF-EF(等式性质),
即AF=BE,
在△ACF和△BDE中,
|
∴△ACF≌△BDE(SAS).
点评:本题主要考查全等三角形的判定和性质,利用三角形全等找到证明全等所需要的条件是解题的关键.

练习册系列答案
相关题目
下列图形中,不是正方体表面展开图的图形的个数是( )


| A、1个 | B、2个 | C、3个 | D、4个 |
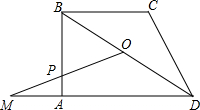 如图,梯形ABCD中,AD∥BC,∠A=90°,BC=CD,点O是对角线BD的中点,BD=5,tan∠DBC=
如图,梯形ABCD中,AD∥BC,∠A=90°,BC=CD,点O是对角线BD的中点,BD=5,tan∠DBC= 如图,已知点A、B、C、D在同一条直线上,AB=CD,CE=DF,∠D=∠ECA,试问:AE与BF的关系,并说明理由.
如图,已知点A、B、C、D在同一条直线上,AB=CD,CE=DF,∠D=∠ECA,试问:AE与BF的关系,并说明理由.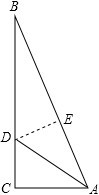 有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求△DEB的面积.
有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求△DEB的面积.