题目内容
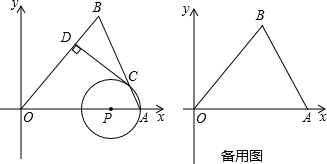
如图,在平面直角坐标系中,点A(10,0)、B(6,8),点P是线段OA上一动点(不与点A重合),以PA为半径的⊙P与线段AB的另一个交点为C,作CD⊥OB于D(如图1).
(1)①BO= ②求证:CD是⊙P的切线;
(2)点G为坐标轴上任意一点,△ABG为直角三角形,求点G的坐标;
(3)当OP=2时,连接PB交CD于F,求DF的长.
(1)①BO=
(2)点G为坐标轴上任意一点,△ABG为直角三角形,求点G的坐标;
(3)当OP=2时,连接PB交CD于F,求DF的长.

考点:圆的综合题
专题:综合题
分析:(1)①根据两点间的距离公式可计算出OB=10,
②连接PC,如图1,由OA=10得OA=OB,根据等腰三角形的性质得∠B=∠OAB,再由PA=PC得到∠PAC=∠PCA,则∠PCA=∠B,根据平行线的判定得到PC∥OB,然后根据平行线的性质由CD⊥OB得到PC⊥OB,再根据切线的判定定理得CD是⊙P的切线;
(2)分类讨论:当G点在x轴上,设G点坐标为(m,0),利用两点间的距离公式得到AB2=(10-6)2+82,AG2=(10-m)2,BG2=(6-m)2+82,若AB2+AG2=BG2,即(10-6)2+82+(10-m)2=(6-m)2+82;若AB2+BG2=AG2,即(10-6)2+82+(6-m)2+82=(10-m)2;若AG2+BG2=AB2,即(10-m)2+(6-m)2+82=(10-6)2+82,然后分别解方程求出m的值得到G点坐标;
当G点在y轴上,设G点坐标为(0,t),同样得到AB2=(10-6)2+82,AG2=102+t2,BG2=62+(t-8)2,也同样得到关于t的方程,解方程求出t即可得到G点坐标;
(3)作BH⊥OA于H,PQ⊥OB于Q,如图2,先计算出AB=4
,利用PC∥OB,根据平行线分线段成比例定理可计算出BC=
,再证明Rt△OQP∽Rt△OHB,
利用相似比计算出PQ=
,易得CD=
;接着在Rt△BDC中利用勾股定理计算出BD=
,然后证明△BDF∽△PCF,利用相似比得
=
,再根据比例的性质可计算出DF.
②连接PC,如图1,由OA=10得OA=OB,根据等腰三角形的性质得∠B=∠OAB,再由PA=PC得到∠PAC=∠PCA,则∠PCA=∠B,根据平行线的判定得到PC∥OB,然后根据平行线的性质由CD⊥OB得到PC⊥OB,再根据切线的判定定理得CD是⊙P的切线;
(2)分类讨论:当G点在x轴上,设G点坐标为(m,0),利用两点间的距离公式得到AB2=(10-6)2+82,AG2=(10-m)2,BG2=(6-m)2+82,若AB2+AG2=BG2,即(10-6)2+82+(10-m)2=(6-m)2+82;若AB2+BG2=AG2,即(10-6)2+82+(6-m)2+82=(10-m)2;若AG2+BG2=AB2,即(10-m)2+(6-m)2+82=(10-6)2+82,然后分别解方程求出m的值得到G点坐标;
当G点在y轴上,设G点坐标为(0,t),同样得到AB2=(10-6)2+82,AG2=102+t2,BG2=62+(t-8)2,也同样得到关于t的方程,解方程求出t即可得到G点坐标;
(3)作BH⊥OA于H,PQ⊥OB于Q,如图2,先计算出AB=4
| 5 |
4
| ||
| 5 |
利用相似比计算出PQ=
| 8 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
| DF |
| FC |
| 1 |
| 10 |
解答:(1)①解 :∵B点坐标为(6,8),
:∵B点坐标为(6,8),
∴OB=
=10,
故答案为10;
②连接PC,如图1,
∵点A(10,0),
∴OA=10,
∴OA=OB,
∴∠B=∠OAB,
∵PA=PC,
∴∠PAC=∠PCA,
∴∠PCA=∠B,
∴PC∥OB,
∵CD⊥OB,
∴PC⊥OB,
∴CD是⊙P的切线;
(2)解:当G点在x轴上,设G点坐标为(m,0),
而A(10,0),B(6,8),则AB2=(10-6)2+82,AG2=(10-m)2,BG2=(6-m)2+82,
若AB2+AG2=BG2,即(10-6)2+82+(10-m)2=(6-m)2+82,解得m=10(舍去);
若AB2+BG2=AG2,即(10-6)2+82+(6-m)2+82=(10-m)2,解得m=-10,此时G点坐标为(-10,0);
若AG2+BG2=AB2,即(10-m)2+(6-m)2+82=(10-6)2+82,解得m1=10(舍去),m2=6,此时G点坐标为(6,0);
当G点在y轴上,设G点坐标为(0,t),则AB2=(10-6)2+82,AG2=102+t2,BG2=62+(t-8)2,
若AB2+AG2=BG2,即(10-6)2+82+102+t2=62+(t-8)2,解得t=-5,此时G点坐标为(0,-5);
若AB2+BG2=AG2,即(10-6)2+82+62+(t-8)2=102+t2,解得t=5,此时G点坐标为(0,5);
若AG2+BG2=AB2,即102+t2+62+(t-8)2=(10-6)2+82,此方程无解,
综上所述,点G的坐标为(-10,0)、(6,0)、(0,-5)、(0,5);
(3)解:作BH⊥OA于H,PQ⊥OB于Q,如图2, ∵OP=2,
∵OP=2,
∴PA=10-2=8,
∴PC=8,
∵A(10,0),B(6,8),
∴AB=
=4
,
∵PC∥OB,
∴
=
,即
=
,解得BC=
,
∵∠POQ=∠BOH,
∴Rt△OQP∽Rt△OHB,
∴
=
,即
=
,解得PQ=
,
∵CD⊥OB,PC⊥CD,
∴四边形PCDQ为矩形,
∴CD=PQ=
,
在Rt△BDC中,∵CD=
,BC=
,
∴BD=
=
,
∵BD∥PC,
∴△BDF∽△PCF,
∴
=
=
=
,
∴
=
,即
=
∴DF=
.
 :∵B点坐标为(6,8),
:∵B点坐标为(6,8),∴OB=
| 62+82 |
故答案为10;
②连接PC,如图1,
∵点A(10,0),
∴OA=10,
∴OA=OB,
∴∠B=∠OAB,
∵PA=PC,
∴∠PAC=∠PCA,
∴∠PCA=∠B,
∴PC∥OB,
∵CD⊥OB,
∴PC⊥OB,
∴CD是⊙P的切线;
(2)解:当G点在x轴上,设G点坐标为(m,0),
而A(10,0),B(6,8),则AB2=(10-6)2+82,AG2=(10-m)2,BG2=(6-m)2+82,
若AB2+AG2=BG2,即(10-6)2+82+(10-m)2=(6-m)2+82,解得m=10(舍去);
若AB2+BG2=AG2,即(10-6)2+82+(6-m)2+82=(10-m)2,解得m=-10,此时G点坐标为(-10,0);
若AG2+BG2=AB2,即(10-m)2+(6-m)2+82=(10-6)2+82,解得m1=10(舍去),m2=6,此时G点坐标为(6,0);
当G点在y轴上,设G点坐标为(0,t),则AB2=(10-6)2+82,AG2=102+t2,BG2=62+(t-8)2,
若AB2+AG2=BG2,即(10-6)2+82+102+t2=62+(t-8)2,解得t=-5,此时G点坐标为(0,-5);
若AB2+BG2=AG2,即(10-6)2+82+62+(t-8)2=102+t2,解得t=5,此时G点坐标为(0,5);
若AG2+BG2=AB2,即102+t2+62+(t-8)2=(10-6)2+82,此方程无解,
综上所述,点G的坐标为(-10,0)、(6,0)、(0,-5)、(0,5);
(3)解:作BH⊥OA于H,PQ⊥OB于Q,如图2,
 ∵OP=2,
∵OP=2,∴PA=10-2=8,
∴PC=8,
∵A(10,0),B(6,8),
∴AB=
| (10-6)2+82 |
| 5 |
∵PC∥OB,
∴
| BC |
| AB |
| OP |
| OA |
| BC | ||
4
|
| 2 |
| 10 |
4
| ||
| 5 |
∵∠POQ=∠BOH,
∴Rt△OQP∽Rt△OHB,
∴
| PQ |
| BH |
| OP |
| OB |
| PQ |
| 8 |
| 2 |
| 10 |
| 8 |
| 5 |
∵CD⊥OB,PC⊥CD,
∴四边形PCDQ为矩形,
∴CD=PQ=
| 8 |
| 5 |
在Rt△BDC中,∵CD=
| 8 |
| 5 |
4
| ||
| 5 |
∴BD=
| BC2-CD2 |
| 4 |
| 5 |
∵BD∥PC,
∴△BDF∽△PCF,
∴
| DF |
| FC |
| BD |
| PC |
| ||
| 8 |
| 1 |
| 10 |
∴
| DF |
| DF+FC |
| 1 |
| 1+10 |
| DF | ||
|
| 1 |
| 11 |
∴DF=
| 8 |
| 55 |
点评:本题考查了圆的综合题:熟练掌握切线的判定定理、等腰三角形的性质;会运用勾股定理、两点间的距离公式和相似比计算线段的长;理解坐标与图形性质;会运用分类讨论的思想解决数学问题.

练习册系列答案
相关题目
下列图形中,不是正方体表面展开图的图形的个数是( )


| A、1个 | B、2个 | C、3个 | D、4个 |
数-5与-4的和比它们的绝对值的和( )
| A、大9 | B、小9 | C、小18 | D、相等 |
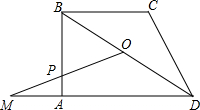 如图,梯形ABCD中,AD∥BC,∠A=90°,BC=CD,点O是对角线BD的中点,BD=5,tan∠DBC=
如图,梯形ABCD中,AD∥BC,∠A=90°,BC=CD,点O是对角线BD的中点,BD=5,tan∠DBC=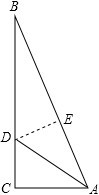 有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求△DEB的面积.
有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求△DEB的面积.