题目内容
11.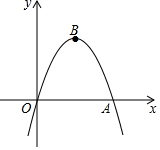 如图,在平面直角坐标系中,抛物线y=-x2+bx与x轴正半轴交于点A,顶点为B,当存在以AB为边,以点O为对称中心的矩形时,b的值为2$\sqrt{3}$.
如图,在平面直角坐标系中,抛物线y=-x2+bx与x轴正半轴交于点A,顶点为B,当存在以AB为边,以点O为对称中心的矩形时,b的值为2$\sqrt{3}$.
分析 由矩形的性质知OB=AB、结合抛物线对称性知△OAB为等边三角形,作BE⊥OA于点E,则BE=$\sqrt{3}$OE,据此可得$\frac{{b}^{2}}{4}$=$\sqrt{3}$•$\frac{b}{2}$,解之即可.
解答 解:如图,作△OCD与△OAB关于原点O中心对称,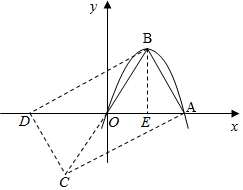
则四边形ABCD为平行四边形,
当OA=OB时,平行四边形ABCD为矩形,
由抛物线的对称性知OB=AB,
∴△OAB为等边三角形,
作BE⊥OA于点E,
则BE=$\sqrt{3}$OE,
∵y=-x2+bx=-(x-$\frac{b}{2}$)2+$\frac{{b}^{2}}{4}$,
则点B($\frac{b}{2}$,$\frac{{b}^{2}}{4}$)
∴$\frac{{b}^{2}}{4}$=$\sqrt{3}$•$\frac{b}{2}$(b>0),
解得:b=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题主要考查抛物线与x轴的交点,熟练掌握矩形的性质及二次函数的图象和性质是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
1.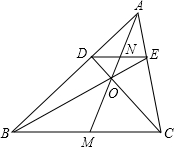 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )| A. | $\frac{DN}{BM}$=$\frac{AD}{AB}$ | B. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ | C. | $\frac{DO}{OC}$=$\frac{DE}{BC}$ | D. | $\frac{AE}{EC}$=$\frac{AO}{OM}$ |
1.函数y=$\frac{{x}^{2}-1}{x-1}$的自变量x的取值范围是 ( )
| A. | x≠0 | B. | x≠1 | C. | x≥1 | D. | x≤1 |
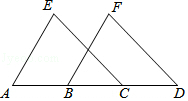 已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.
已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.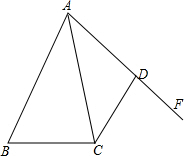 如图,己知AB>AD,∠BAC=∠FAC,CD=BC,求证:∠ADC+∠B=180°.
如图,己知AB>AD,∠BAC=∠FAC,CD=BC,求证:∠ADC+∠B=180°. 如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=130°,则∠C=130度.
如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=130°,则∠C=130度.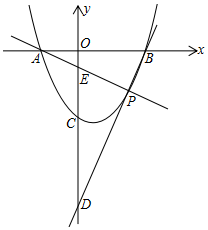 如图,已知抛物线y=x2-(2m+1)x+m2+m-2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,P(s,t)为抛物线上A、B之间一点(不包括A、B),连接AP、BP分别交y轴于点E、D
如图,已知抛物线y=x2-(2m+1)x+m2+m-2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,P(s,t)为抛物线上A、B之间一点(不包括A、B),连接AP、BP分别交y轴于点E、D