题目内容
9．下列说法中，正确的是（ ）| A． | 无理数包括正无理数，0和负无理数 | B． | 无理数是用根号形式表示的数 | ||
| C． | 无理数的和一定是无理数 | D． | 无理数是无限不循环小数 |
分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解答 解：A、无理数包括正无理数和负无理数，故A错误；
B、无理数是无限不循小数，故B错误；
C、2π+（5-2π）=5，故C错误；
D、无理数是无限不循小数，故D正确；
故选：D．
点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
练习册系列答案
相关题目
17．
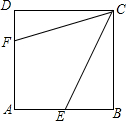如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若点E为AB的中点，且满足BE+DF=EF，则EF的长为（ ）
如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若点E为AB的中点，且满足BE+DF=EF，则EF的长为（ ）| A． | 4 | B． | 3$\sqrt{2}$ | C． | 5 | D． | 4$\sqrt{2}$ |
4．使分式$\frac{a+1}{a-1}$有意义的a的取值范围为（ ）
| A． | a＜1 | B． | a＞1 | C． | a≠1 | D． | a=1 |
1．已知点A（3，a），B（-1，b），C （-2，c）都在函数y=$\frac{4}{x}$的图象上，则a、b、c的大小关系是（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞b＞a | D． | a＞c＞b |
18．
如图，点P是直线y=$\frac{1}{2}$x+1上动点，点Q（0，m）是y轴负半轴上定点，连接PQ，当PQ的长度最小时，∠PQO的正弦值为（ ）
如图，点P是直线y=$\frac{1}{2}$x+1上动点，点Q（0，m）是y轴负半轴上定点，连接PQ，当PQ的长度最小时，∠PQO的正弦值为（ ）| A． | $\frac{{2\sqrt{5}}}{5}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{1}{2}$ | D． | 和m的取值有关 |
19．已知整式x2-2x的值为-1，则x2-2x+3的值为（ ）
| A． | -2 | B． | 2 | C． | -4 | D． | 4 |