题目内容
3. 证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
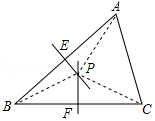
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴PB=PA.
同理可得,PB=PC.
∴PA=PC(等量代换).
∴点P是AC边垂直平线上的一点.(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
∴AB、BC、AC的垂直平分线交于点P.
分析 根据线段垂直平分线的性质即可得到结论.
解答 证明:∵点P是AB边垂直平线上的一点,
∴PB=PA.
同理可得,PB=PC.
∴PA=PC(等量代换).
∴点P是AC边垂直平线上的一点.(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
∴AB、BC、AC的垂直平分线交于点P.
故答案为:PB,PA,PC,PA,PC,点P是AC边垂直平线上的一点.
点评 本题考查了线段垂直平分线的性质,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
相关题目
15.已知点P1(1,y1)和P2(3,y2)是一次函数y=-2x+1图象上的两个点,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 以上都不对 |
 如图,在△ABC中,AD、BE分别是BC、AC边上的高.求证:△DCE∽△ACB.
如图,在△ABC中,AD、BE分别是BC、AC边上的高.求证:△DCE∽△ACB.