题目内容
8.若|a|=21,b2=36,且a<b,则|a-b|=15或27.分析 要计算a与b差的绝对值,首先计算出a,b.需根据绝对值和平方根的意义,以及a、b关系,确定a、b的值.
解答 解:因为|a|=21,所以a=±21;
因为b2=36,所以b=±6.
当a=-21,b=6时,满足a<b,|a+b|=|-21+6|=|-15|=15;
当a=-21,b=-6时,满足a<b,||a+b|=|-21-6|=|-27|=27.
故答案为:15或27.
点评 本题考查了绝对值的意义、平方根的定义及有理数的计算.解决本题,根据a<b确定a、b的值并分类讨论是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.在$\frac{1}{2}$,0,-$\frac{1}{3}$,-$\frac{1}{2}$这四个数中,最小的数是( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
13.在平面直角坐标系中点A(a,4)与点B(-5,b)关于y轴对称,则2a+b的值为( )
| A. | 14 | B. | 2 | C. | -14 | D. | -2 |
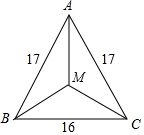 如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,求AM的长度为10.
如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,求AM的长度为10.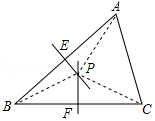 证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.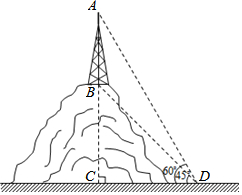 如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).
如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).