题目内容
13.现在有4个小长方体纸盒,每个的长、宽、高都分别是16cm,6cm,2cm,若将这4个纸盒搭成一个大长方体,共有3种不同的方式,搭成的大长方体的表面积最小为608cm2.分析 要使表面积最小,那就是把4个长方体的最大面,即16×6重合,这个长方体的表面积用4个小长方体的表面积之和减去8个重合的面的面积;根据长方体的表面积公式:S=2(ab+ah+bh),把数据代入公式解答.
解答  解:由题意可知,有三种搭法,其中要搭成的大长方体的表面积最小,如图所示,让小长方体的最大面重合;
解:由题意可知,有三种搭法,其中要搭成的大长方体的表面积最小,如图所示,让小长方体的最大面重合;
其表面积为:S=4×2×(16×6+16×2+2×6)-16×6×4-16×2×4,
=1120-384-128,
=608,
答:搭成的大长方体的表面积最小为608cm2.
故答案为:608.
点评 此题主要考查了长方体的表面积的计算,明确把四个相同的长方体拼成一个大的长方体,有三种情况,其中最小的面重合时,拼成的表面积最大,最大的面重合时,拼成的表面积最小.

练习册系列答案
相关题目
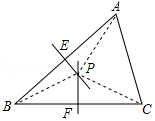 证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.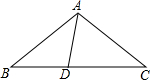 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC.
如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC.