题目内容
4.从一块半径是4m的圆形铁片上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )| A. | $\sqrt{2}$m | B. | 2m | C. | 4m | D. | $\sqrt{15}$m |
分析 设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=$\frac{90•π•4}{180}$,解得r=1,然后利用勾股定理计算圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{90•π•4}{180}$,解得r=1,
所以圆锥的高=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$(m).
故选D.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
14.计算a5•(-$\frac{1}{a}$)2的结果是( )
| A. | -a3 | B. | a3 | C. | a7 | D. | a10 |
12.使式子$\sqrt{1-a}$有意义的a的范围是( )
| A. | a≥0 | B. | a≤0 | C. | a≥1 | D. | a≤1 |
9.已知一个正n边形的一个内角是它外角的5倍,则n等于( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
13.脸谱是中国戏曲演员脸上的绘画,用于舞台演出时的化妆造型,助增所扮演人物的性格和特征.在下列八张脸谱图片中,随机抽取一张为 的概率是( )
的概率是( )

 的概率是( )
的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{8}$ |
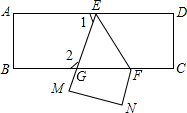 如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数.
如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数.