题目内容
11.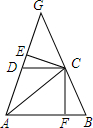 如图,△ABC中,AB∥DC,AD=DC=CH,AD,BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F,求证:DE=BF.
如图,△ABC中,AB∥DC,AD=DC=CH,AD,BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F,求证:DE=BF.
分析 由等腰梯形的性质和平行线的性质得出∠DAB=∠B,∠EDC=∠DAB,得出∠EDC=∠B,由AAS证明△CDE≌△CBF,得出对应边相等即可.
解答 证明:∵AB∥DC,AD=CB,
∴四边形ABCD是等腰梯形,
∴∠DAB=∠B,∠EDC=∠DAB,
∴∠EDC=∠B,
∵CE⊥AG于E,CF⊥AB于F,
∴∠DEC=∠BFC=90°,
在△CDE和△CBF中,$\left\{\begin{array}{l}{∠EDC=∠B}&{\;}\\{∠DEC=∠BFC}&{\;}\\{CD=CB}&{\;}\end{array}\right.$,
∴△CDE≌△CBF(AAS),
∴DE=BF.
点评 本题考查了等腰梯形的判定与性质、全等三角形的判定与性质、平行线的性质;熟练掌握等腰梯形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图,AB为⊙O的直径,P为AB延长线上一点,PC与⊙O相切于点C,∠P的平分线交BC、AC于点D、E.则下列结论不正确的是( )
如图,AB为⊙O的直径,P为AB延长线上一点,PC与⊙O相切于点C,∠P的平分线交BC、AC于点D、E.则下列结论不正确的是( )
 如图,AB为⊙O的直径,P为AB延长线上一点,PC与⊙O相切于点C,∠P的平分线交BC、AC于点D、E.则下列结论不正确的是( )
如图,AB为⊙O的直径,P为AB延长线上一点,PC与⊙O相切于点C,∠P的平分线交BC、AC于点D、E.则下列结论不正确的是( )| A. | △PBC∽△PCA | B. | △PCD∽△PAE | ||
| C. | △CDE是等腰直角三角形 | D. | 点E、F三等分AC |
1.99$\frac{18}{19}×15=(100-\frac{1}{19})×15=1500-\frac{15}{19}$,这个运算应用了( )
| A. | 加法交换律 | B. | 乘法结合律 | ||
| C. | 乘法交换律、乘法结合律 | D. | 乘法分配律 |
 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B,二次函数的图象与y轴相交于点C,与直线y=$\frac{1}{2}$x+1相交于点A、D,CD∥x轴,∠CDA=∠OCA.
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别相交于点A、B,二次函数的图象与y轴相交于点C,与直线y=$\frac{1}{2}$x+1相交于点A、D,CD∥x轴,∠CDA=∠OCA.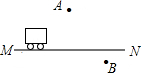 如图所示,一辆汽车在平直的公路上由M向N方向行驶,A、B分别是位于公路MN两侧的村庄.
如图所示,一辆汽车在平直的公路上由M向N方向行驶,A、B分别是位于公路MN两侧的村庄.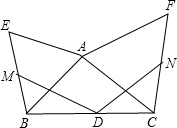 如图,D为△ABC的边BC的中点,△ABE,△ACF均为正三角形,M,N分别为BE,CF的中点,求∠MDN的度数.
如图,D为△ABC的边BC的中点,△ABE,△ACF均为正三角形,M,N分别为BE,CF的中点,求∠MDN的度数.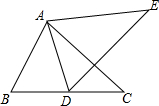 如图,AB=AD,∠BAD=∠EAC,∠C=∠E,求证:AE=AC.
如图,AB=AD,∠BAD=∠EAC,∠C=∠E,求证:AE=AC.