题目内容
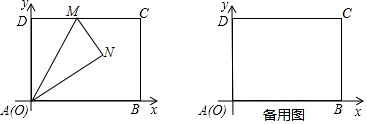
10. 如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
分析 (1)证明三个角是直角即可解决问题;
(2)结论:MN∥BC且MN=$\frac{1}{2}$BC.只要证明MN是△ABC的中位线即可;
(3)△ABC是直角三角形(∠ACB=90°);
解答 (1)证明:∵AE⊥CE于E,AF⊥CF于F,
∴∠AEC=∠AFC=90°,
又∵CE、CF分别平分∠ACB与它的邻补角∠ACD,
∴∠BCE=∠ACE,∠ACF=∠DCF,
∴∠ACE+∠ACF=$\frac{1}{2}$(∠BCE+∠ACE+∠ACF+∠DCF)=$\frac{1}{2}$×180°=90°,
∴三个角为直角的四边形AECF为矩形.
(2)结论:MN∥BC且MN=$\frac{1}{2}$BC.
证明:∵四边形AECF为矩形,
∴对角线相等且互相平分,
∴NE=NC,
∴∠NEC=∠ACE=∠BCE,
∴MN∥BC,
又∵AN=CN(矩形的对角线相等且互相平分),
∴N是AC的中点,
若M不是AB的中点,则可在AB取中点M1,连接M1N,
则M1N是△ABC的中位线,MN∥BC,
而MN∥BC,M1即为点M,
所以MN是△ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)
∴MN=$\frac{1}{2}$BC;
法二:延长MN至K,使NK=MN,
因为对角线互相平分,
所以AMCK是平行四边形,KC∥MA,KC=AM因为MN∥BC,
所以MBCK是平行四边形,MK=BC,
所以MN=$\frac{1}{2}$BC
(3)解:△ABC是直角三角形(∠ACB=90°).
理由:∵四边形AECF是菱形,
∴AC⊥EF,
∵EF∥AC,
∴AC⊥CB,
∴∠ACB=90°.即△ABC是直角三角形.
点评 本题考查矩形的判定和性质、菱形的性质.三角形的中位线定理、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{4a+4}$ |
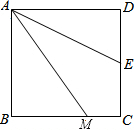 如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.
如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM. 如图,在Rt△ABC中,∠C=90°.以点A为圆心、AC长为半径作圆弧,交边AB于点D.若∠B=65°,AC=6,则$\widehat{CD}$的长为$\frac{5}{6}$π.
如图,在Rt△ABC中,∠C=90°.以点A为圆心、AC长为半径作圆弧,交边AB于点D.若∠B=65°,AC=6,则$\widehat{CD}$的长为$\frac{5}{6}$π. 如图,在?ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
如图,在?ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.