题目内容
19. 如图,在?ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
如图,在?ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
分析 (1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,即可证明DE∥BF,
(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=$\frac{1}{2}$AB,DF=$\frac{1}{2}$CD.
∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形,
∴DE∥BF;
(2)∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DEBF是平行四边形,
∴四边形DEBF是菱形.
点评 本题主要考查了平行四边形的性质、菱形的判定,直角三角形的性质:在直角三角形中斜边中线等于斜边一半,比较综合,难度适中.

练习册系列答案
相关题目
7.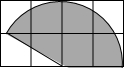 如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为$\frac{5}{3}$π;小亮说此圆锥的弧长为$\frac{5}{3}$π,则下列结论正确的是( )
如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为$\frac{5}{3}$π;小亮说此圆锥的弧长为$\frac{5}{3}$π,则下列结论正确的是( )
 如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为$\frac{5}{3}$π;小亮说此圆锥的弧长为$\frac{5}{3}$π,则下列结论正确的是( )
如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为$\frac{5}{3}$π;小亮说此圆锥的弧长为$\frac{5}{3}$π,则下列结论正确的是( )| A. | 只有小明对 | B. | 只有小亮对 | C. | 两人都对 | D. | 两人都不对 |
14. 二次函数y=3(x-h)2+k的图象如图所示,下列判断正确的是( )
二次函数y=3(x-h)2+k的图象如图所示,下列判断正确的是( )
 二次函数y=3(x-h)2+k的图象如图所示,下列判断正确的是( )
二次函数y=3(x-h)2+k的图象如图所示,下列判断正确的是( )| A. | h>0,k>0 | B. | h>0,k<0 | C. | h<0,k>0 | D. | h<0,k<0 |
11.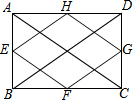 如图,已知矩形ABCD的对角线AC,BD的长是6cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长是( )
如图,已知矩形ABCD的对角线AC,BD的长是6cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长是( )
 如图,已知矩形ABCD的对角线AC,BD的长是6cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长是( )
如图,已知矩形ABCD的对角线AC,BD的长是6cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长是( )| A. | 18cm | B. | 16cm | C. | 15cm | D. | 12cm |
 如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N. 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=4,BC=6,将四个直角三角形中边长为4的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=4,BC=6,将四个直角三角形中边长为4的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )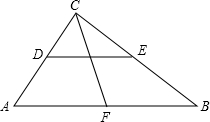 如图,在Rt△ABC中,∠ACB=90°,点F是AB的中点,CF=8cm,则中位线DE=8cm.
如图,在Rt△ABC中,∠ACB=90°,点F是AB的中点,CF=8cm,则中位线DE=8cm.