题目内容
11. 如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )| A. | 2S | B. | 1.5S | C. | 1.2S | D. | 1.8S |
分析 在AB上分别截取AF=AE,BG=BD,连结OF、OG、EF,EF交AO于M,作FH⊥OG于H,如图,先证明△AEO≌△AFO得到S△AEO=S△AFO,同理可得S△BDO=S△BGO,再利用AD平分∠CAB,BE平分∠CBA得到∠OAB+∠OBA=$\frac{1}{2}$∠CAB+$\frac{1}{2}$∠CBA=45°,由于△AEO≌△AFO得到OE=OF,∠EOA=∠FOA=45°,于是得到∠EOF=90°,△OEF为等腰直角三角形,OM⊥EF,根据等腰直角三角形的性质得OM=EM=MF,同理可得∠DOG=90°,所以四边形OMFH为正方形,所以FH=OM=EM,利用三角形面积公式得到S△OFG=S△OED,于是得到四边形ABDE的面积=2S△AOB=2S.
解答 解:在AB上分别截取AF=AE,BG=BD,连结OF、OG、EF,EF交AO于M,作FH⊥OG于H,如图,
∵AD平分∠CAB,
∴∠EAO=∠FAO,
在△AEO和△AFO中,
$\left\{\begin{array}{l}{AE=AF}\\{∠EAO=∠FAO}\\{AO=AO}\end{array}\right.$,
∴△AEO≌△AFO,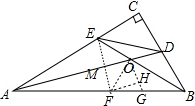
∴S△AEO=S△AFO,
同理可得S△BDO=S△BGO,
∵AD平分∠CAB,BE平分∠CBA,
∴∠OAB+∠OBA=$\frac{1}{2}$∠CAB+$\frac{1}{2}$∠CBA=45°,
∵△AEO≌△AFO,
∴OE=OF,∠EOA=∠FOA=45°,
∴∠EOF=90°,△OEF为等腰直角三角形,
∴OM⊥EF,
∴OM=EM=MF,
同理可得∠DOG=90°,
∴四边形OMFH为正方形,
∴FH=OM=EM,
∵S△OFG=$\frac{1}{2}$FH•OG,S△OED=$\frac{1}{2}$•OD•EM,
∴S△OFG=S△OED,
∴四边形ABDE的面积=2S△AOB=2S.
故选A.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.解决本题的关键是把△AOB分成三个三角形,分别证明S△AEO=S△AFO,S△BDO=S△BGO,S△OFG=S△OED.

 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
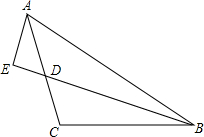 如图,在△ABC中,AC=BC,∠ABC=90°,D是AC的中点,且AE=$\frac{1}{2}$BD,求证:BE是∠ABC的角平分线.
如图,在△ABC中,AC=BC,∠ABC=90°,D是AC的中点,且AE=$\frac{1}{2}$BD,求证:BE是∠ABC的角平分线. 如图所示,在直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(2,3),B(5,4),C(8,2),试确定这个四边形的面积.
如图所示,在直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(2,3),B(5,4),C(8,2),试确定这个四边形的面积.