题目内容
19.已知:Rt△ABD与△CBD位于BD的两侧(如图1),且∠ABD=90°,∠ADB=30°,AD=8,∠BCD=90°,∠BDC=45°,点O在AD边上,连接BO沿直线BO翻折△ABO至△A′BO.(1)如图2,当点A′落在BC边上,求∠OBD的度数;
(2)如图3,当点A′落在AD边上,连接A′C,求证:A′C∥AB.
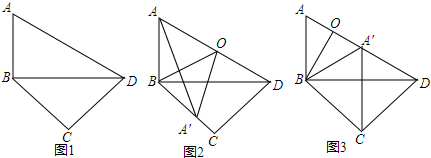
分析 (1)根据三角形的内角和得到∠DAB=60°,∠CBD=45°,于是得到∠ABC=135°,根据折叠的性质得到AB=A′B,AA′⊥BO,于是求得∠ABO=$\frac{1}{2}∠$ABC=67.5°,即可得到结论;
(2)根据折叠的性质得到AB=A′B,AA′⊥BO,AO=A′O,推出△AA′B是等边三角形,根据等边三角形的性质得到AA′=AB,根据直角三角形的性质得到AB=AA′=$\frac{1}{2}$AD=4,求出A′B=A′D,于是得到A′C⊥BD,根据平行线的判定定理即可得到结论.
解答 解:(1)∵∠ABD=90°,∠ADB=30°,
∴∠DAB=60°,
∵∠BCD=90°,∠BDC=45°,
∴∠CBD=45°,
∴∠ABC=135°,
∵沿直线BO翻折△ABO至△A′BO,
∴AB=A′B,AA′⊥BO,
∴∠ABO=$\frac{1}{2}∠$ABC=67.5°,
∴∠OBD=∠ABD-∠ABO=22.5°;
(2)∵沿直线BO翻折△ABO至△A′BO,
∴AB=A′B,AA′⊥BO,AO=A′O,
∵∠A=60°,
∴△AA′B是等边三角形,
∴AA′=AB,
∵∠ABD=90°,∠ADB=30°,
∴AB=AA′=$\frac{1}{2}$AD=4,
∴A′D=4,
∴A′B=A′D,
∵BC=DC,
∴A′C⊥BD,
∵AB⊥BD,
∴A′C∥AB.
点评 本题考查了翻折变换-折叠问题,直角三角形的性质,线段垂直平分线的判定和性质,等边三角形的判定和性质,熟练掌握折叠的性质是解题的关键.

练习册系列答案
相关题目
11. 如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
 如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )| A. | 2S | B. | 1.5S | C. | 1.2S | D. | 1.8S |
8.关于x的方程x2+2x-k=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | k<1 | D. | k<1且k≠0 |
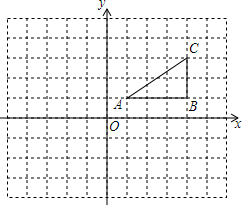 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,已知△ABC:
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,已知△ABC: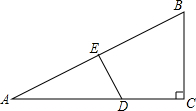 已知,如图,在Rt△ABC中,斜边AB的垂直平分线分别交AC,AB于点D,E,AE=BC,求证:AD=2CD.
已知,如图,在Rt△ABC中,斜边AB的垂直平分线分别交AC,AB于点D,E,AE=BC,求证:AD=2CD.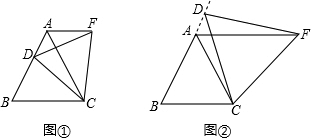
 如图,OP为∠AOB内一条射线,C、D分别为OA、OB上两点,且∠PCO+∠PDO=180°,PC=PD.求证:OP平分∠A0B.
如图,OP为∠AOB内一条射线,C、D分别为OA、OB上两点,且∠PCO+∠PDO=180°,PC=PD.求证:OP平分∠A0B. 已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.
已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.