题目内容
20．若方程组$\left\{\begin{array}{l}{3x+y=1+3a}\\{x+3y=1-a}\end{array}\right.$的解满足x+y=0，则a的值为（ ）| A． | -1 | B． | 1 | C． | 0 | D． | 无法确定 |
分析 方程组两方程相加表示出x+y，代入x+y=0求出a的值即可．
解答 解：方程组两方程相加得：4（x+y）=2+2a，即x+y=$\frac{1}{2}$（1+a），
由x+y=0，得到$\frac{1}{2}$（1+a）=0，
解得：a=-1．
故选A．
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
练习册系列答案
备战中考寒假系列答案
相关题目
11．
如图，在△ABC中，∠C=90°，AD平分∠CAB，BE平分∠CBA，AD、BE相交于点O，若△AOB的面积为S，则四边形ABDE的面积为（ ）
如图，在△ABC中，∠C=90°，AD平分∠CAB，BE平分∠CBA，AD、BE相交于点O，若△AOB的面积为S，则四边形ABDE的面积为（ ）| A． | 2S | B． | 1.5S | C． | 1.2S | D． | 1.8S |
8．关于x的方程x2+2x-k=0有两个不相等的实数根，则k的取值范围是（ ）
| A． | k＞-1 | B． | k＞-1且k≠0 | C． | k＜1 | D． | k＜1且k≠0 |
已知：如图，有一块面积等于1200cm2的三角形纸片ABC，已知底边与底边BC上的高的和为100cm（底边BC大于底边上的高），要把它加工成一个正方形纸片，使正方形的一边EF在边BC上，顶点D、G分别在边AB、AC上，求加工成的正方形铁片DEFG的边长．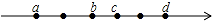
数轴上有六个点，每相邻的两个点间的距离都是1个单位长度，有理数a、b、c、d所对应的点是这些点中的4个，位置如图所示．