题目内容
1.若一次函数y=kx+b的图象与y轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,则此一次函数的表达式为y=2x-2或y=-2x-2.分析 根据题意,画出一次函数y=kx+b的大体图象所在的位置,然后根据直角三角形的面积公式求得该函数图象与x轴的交点,再将其代入函数解析式,求得k值.
解答 解:根据题意,知一次函数y=kx+b的图象如图所示:
∵S△AOC=1,OC=2,
∴1=$\frac{1}{2}$×OA•OC,
∴OA=1;
①∴一次函数y=kx+b的图象经过点(0,-2)、(-1,0),
∴$\left\{\begin{array}{l}{-k+b=0}\\{b=-2}\end{array}\right.$,
解得,k=-2,
∴一次函数的表达式是y=-2x-2;
②同理求得OB=1,
∴一次函数y=kx+b的图象经过点(0,-2)、(1,0),
$\left\{\begin{array}{l}{k+b=0}\\{b=-2}\end{array}\right.$,
∴k=2,
∴一次函数的表达式是y=2x-2.
故答案为:y=2x-2或y=-2x-2;
点评 本题考查了用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,注意:一次函数图象上的点,一定满足该函数的关系式,题目比较好,注意要进行分类讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
 如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )| A. | 2S | B. | 1.5S | C. | 1.2S | D. | 1.8S |
 已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.
已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.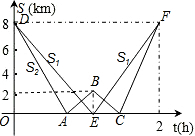 在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),下图中的折线分别表示S1、S2与t之间的函数关系.
在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),下图中的折线分别表示S1、S2与t之间的函数关系. 如图,点C、D是线段AB上的两点,若AC=4,CD=8,DB=3,
如图,点C、D是线段AB上的两点,若AC=4,CD=8,DB=3,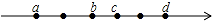 数轴上有六个点,每相邻的两个点间的距离都是1个单位长度,有理数a、b、c、d所对应的点是这些点中的4个,位置如图所示.
数轴上有六个点,每相邻的两个点间的距离都是1个单位长度,有理数a、b、c、d所对应的点是这些点中的4个,位置如图所示.