题目内容
6.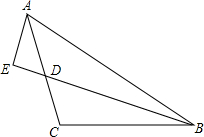 如图,在△ABC中,AC=BC,∠ABC=90°,D是AC的中点,且AE=$\frac{1}{2}$BD,求证:BE是∠ABC的角平分线.
如图,在△ABC中,AC=BC,∠ABC=90°,D是AC的中点,且AE=$\frac{1}{2}$BD,求证:BE是∠ABC的角平分线.
分析 延长AE、BC交于点F.根据同角的余角相等,得∠DBC=∠FAC;在△BCD和△ACF中,根据ASA证明全等,得AF=BD,从而AE=EF,根据线段垂直平分线的性质,得AB=BF,再根据等腰三角形的三线合一即可证明.
解答 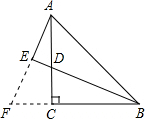 证明:延长AE、BC交于点F;如图所示:
证明:延长AE、BC交于点F;如图所示:
∵AE⊥BE,
∴∠BEF=90°,又∠ACF=∠ACB=90°,
∴∠DBC+∠AFC=∠FAC+∠AFC=90°,
∴∠DBC=∠FAC,
在△ACF和△BCD中,$\left\{\begin{array}{l}{∠ACF=∠BCD}&{\;}\\{AC=BC}&{\;}\\{∠FAC=∠DBC}&{\;}\end{array}\right.$,
∴△ACF≌△BCD(ASA),
∴AF=BD.
又AE=$\frac{1}{2}$BD,
∴AE=EF,即点E是AF的中点.
∴AB=BF,
∴BD是∠ABC的角平分线.
点评 此题综合运用了全等三角形的判定以及性质、线段垂直平分线的性质以及等腰三角形的判定与性质;熟练掌握等腰三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
 如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点O,若△AOB的面积为S,则四边形ABDE的面积为( )| A. | 2S | B. | 1.5S | C. | 1.2S | D. | 1.8S |


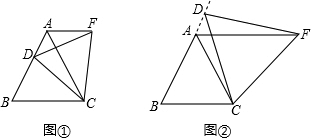
 如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,延长BA、CE相交于点F.求证:BD=2CE.
如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,延长BA、CE相交于点F.求证:BD=2CE.