题目内容
8.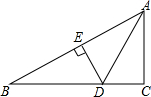 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,求DE的长.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,求DE的长.
分析 根据线段垂直平分线的性质得到DB=DA,得到∠DBA=∠DAB,根据角平分线的定义得到∠CAD=∠DAB,求出∠B=30°,计算即可.
解答 解:∵DE是AB的垂直平分线,
∴DB=DA,
∴∠DBA=∠DAB,
∵BC是∠CAB的平分线,
∴∠CAD=∠DAB,
∴∠DBA=∠DAB=∠CAD=30°,
∴DE=$\frac{1}{2}$BD,
∵BC是∠CAB的平分线,∠C=90°,DE⊥AB,
∴DC=DE=$\frac{1}{2}$BC,
∴DE=1.
点评 本题考查的是线段垂直平分线的性质、角平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
表1 阅读课外书籍人数分组统计表
请你根据以上信息解答下列问题:
(1)这次共调查了学生多少人?
(2)E组人数在这次调查中所占的百分比是多少?
(3)求出表1中a的值,并补全图1;
(4)若该年级共有学生300人,请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人?
 某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.表1 阅读课外书籍人数分组统计表
| 分组 | 阅读课外书籍时间n(小时) | 人数 |
| A | 0≤n<3 | 3 |
| B | 3≤n<6 | 10 |
| C | 6≤n<9 | a |
| D | 9≤n<12 | 13 |
| E | 12≤n<15 | b |
| F | 15≤n<18 | c |
(1)这次共调查了学生多少人?
(2)E组人数在这次调查中所占的百分比是多少?
(3)求出表1中a的值,并补全图1;
(4)若该年级共有学生300人,请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人?
 如图是一座抛物形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降3m时,水面的宽为6$\sqrt{7}$m.
如图是一座抛物形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降3m时,水面的宽为6$\sqrt{7}$m.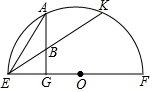 如图,A是以EF为直径的半圆上的一点,作AG⊥EF交EF于G,又B为AG上一点,EB的延长线交半圆于点K,若EB=2,EK=6,则AE=2$\sqrt{3}$.
如图,A是以EF为直径的半圆上的一点,作AG⊥EF交EF于G,又B为AG上一点,EB的延长线交半圆于点K,若EB=2,EK=6,则AE=2$\sqrt{3}$.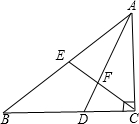 如图,△ABC中,∠ACB=90°,D在BC上,E为AB之中点,AD、CE相交于F,且AD=DB.若∠B=35°,求∠DFE的度数.
如图,△ABC中,∠ACB=90°,D在BC上,E为AB之中点,AD、CE相交于F,且AD=DB.若∠B=35°,求∠DFE的度数. 如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE的度数为90°.
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE的度数为90°.