题目内容
18. 如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE的度数为90°.
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE的度数为90°.
分析 先用HL判断出Rt△ABC≌Rt△CDE(HL),即可得出∠ACB=∠CED,再用同角的余角相等即可得出结论.
解答 解:∵AB⊥BD,ED⊥BD,
∴∠ABC=∠CDE=90°,
在Rt△ABC和Rt△CDE中,$\left\{\begin{array}{l}{AB=CD}\\{AC=CE}\end{array}\right.$,
∴Rt△ABC≌Rt△CDE(HL),
∴∠ACB=∠CED,
∵∠DCE+∠CED=90°,
∴∠ACB+∠DCE=90°,
∴∠ACE=90°.
故答案为:90°.
点评 此题主要考查了全等三角形的判定和性质,同角的余角相等,直角三角形的性质,判断出Rt△ABC≌Rt△CDE(HL),是解本题的关键.

练习册系列答案
相关题目
10.如果代数式$\frac{x-1}{\sqrt{x+2}}$有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x>-2 | C. | x<-2 | D. | x≤-2 |
7.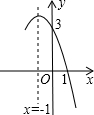 抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
 抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )| A. | -3<x<1 | B. | x<-3或x>1 | C. | -4<x<l | D. | x<-4或x>1 |
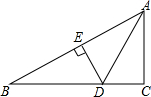 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,求DE的长.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,求DE的长.
 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BFA=34°,则∠DAE=17度.
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BFA=34°,则∠DAE=17度. 如图,点O为平面直角坐标系的原点,点A的坐标为(6,8),点B的坐标为(12,0).
如图,点O为平面直角坐标系的原点,点A的坐标为(6,8),点B的坐标为(12,0).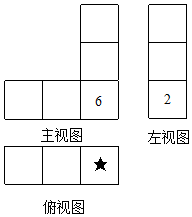 一个不透明立方体的6个面上分别写有数字1、2、3、4、5、6,任意两对面上所写的两个数字之和为7,将这样的几个立方体按照相接触两个面上的数字之和为8,摆放成一个几何体,这个几何体的三视图如图所示,图中所标注的是部分面上所见的数字,则★所代表的数是( )
一个不透明立方体的6个面上分别写有数字1、2、3、4、5、6,任意两对面上所写的两个数字之和为7,将这样的几个立方体按照相接触两个面上的数字之和为8,摆放成一个几何体,这个几何体的三视图如图所示,图中所标注的是部分面上所见的数字,则★所代表的数是( )