题目内容
18.如图,在已知△ABC中,AB=AC,∠BAC=45°,把△ABC绕点C顺时针旋转.(1)如果点B落在边AC上,得△A1B1C,求∠AB1A1的度数;
(2)如果点B落在边AB上,得△A2B2C那么AB与A2C平行吗?请说明理由;
(3)在(2)的条件下,联结AA2,试说明△AB2A2≌△B2AC的理由.
分析 (1)先根据等腰三角形的性质以及旋转的性质,求得∠A1B1C=∠B=67.5°,再根据平角的定义求得∠AB1A1的度数;
(2)先根据等腰三角形的性质以及旋转的性质,求得∠A2CB2=∠ACB=67.5°,进而得到∠CB2B=∠B=67.5°,以及∠B2CB=45°,根据角的和差关系得到∠BCA2=112.5°,从而得出∠B+∠BCA2=180°,进而判定AB∥A2C;
(3)先根据等腰三角形的性质以及旋转的性质,求得∠BAA2+∠B=180°,得出AA2∥BC,再根据AB∥A2C,判定四边形ABCA2是平行四边形,进而得出AA2=BC,再根据CB=CB2,可得AA2=B2C,最后根据SAS即可判定△AB2A2≌△B2AC.
解答 解:(1)如图所示,∵△ABC中,AB=AC,∠BAC=45°,
∴∠B=$\frac{1}{2}$(180°-∠A)=67.5°,
由旋转可得,∠A1B1C=∠B=67.5°,
∴∠AB1A1=180°-∠A1B1C=112.5°;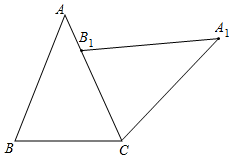
(2)AB∥A2C.
理由:如图所示,在△ABC中,AB=AC,∠BAC=45°,
∴∠ACB=$\frac{1}{2}$(180°-∠BAC)=67.5°,
由旋转可得,CB=CB2,∠A2CB2=∠ACB=67.5°,
∴∠CB2B=∠B=67.5°,
∴旋转角∠B2CB=45°,
∴∠BCA2=45°+67.5°=112.5°,
∴∠B+∠BCA2=180°,
∴AB∥A2C;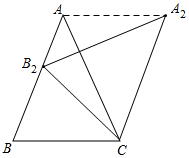
(3)如图所示,连接AA2,
由(2)可得∠CB2B=∠B=67.5°,
∴∠AB2C=180°-67.5°=112.5°,
由旋转可得,∠ACA2=∠B2CB=45°,AC=A2C,
∴△ACA2中,∠CAA2=$\frac{1}{2}$(180°-∠ACA2)=67.5°,
∴∠B2AA2=∠BAC+∠CAA2=45°+67.5°=112.5°,
∴∠BAA2+∠B=112.5°+67.5°=180°,且∠B2AA2=∠AB2C,
∴AA2∥BC,
又∵AB∥A2C,
∴四边形ABCA2是平行四边形,
∴AA2=BC,
又∵CB=CB2,
∴AA2=B2C,
在△AB2A2和△B2AC中,
$\left\{\begin{array}{l}{A{A}_{2}={B}_{2}C}\\{∠{B}_{2}A{A}_{2}=∠A{B}_{2}C}\\{A{B}_{2}={B}_{2}A}\end{array}\right.$,
∴△AB2A2≌△B2AC(SAS).
点评 本题属于三角形综合题,主要考查了等腰三角形的性质,旋转的性质,全等三角形的判定以及平行四边形的判定与性质的综合应用,解决问题的关键是掌握旋转的性质:旋转前、后的图形全等.解题时注意:平行四边形的对边相等.

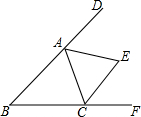 如图,△ABC中,∠B=30°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为75°.
如图,△ABC中,∠B=30°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为75°. 如图,每个小正方形的边长均为1,求图中阴影正方形的面积和边长.
如图,每个小正方形的边长均为1,求图中阴影正方形的面积和边长.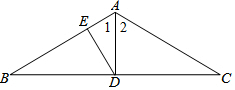 如图,在△ABC中,∠B=∠C=30°,D是BC边上的中点,DE⊥AB于E,BC=12.求:
如图,在△ABC中,∠B=∠C=30°,D是BC边上的中点,DE⊥AB于E,BC=12.求:
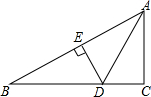 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,求DE的长.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,求DE的长.