题目内容
9.(1)$\sqrt{50}$-$\frac{1}{\sqrt{5}}$+2$\sqrt{20}$-$\sqrt{45}$+$\sqrt{\frac{1}{2}}$(2)($\sqrt{18}$-3$\sqrt{\frac{1}{2}}$)×$\sqrt{6}$.
分析 (1)根据二次根式的混合运算顺序,首先计算开方,然后计算乘法,最后从左向右依次计算,求出算式$\sqrt{50}$-$\frac{1}{\sqrt{5}}$+2$\sqrt{20}$-$\sqrt{45}$+$\sqrt{\frac{1}{2}}$的值是多少即可.
(2)根据算式的特征,应用乘法分配律,求出算式($\sqrt{18}$-3$\sqrt{\frac{1}{2}}$)×$\sqrt{6}$的值是多少即可.
解答 解:(1)$\sqrt{50}$-$\frac{1}{\sqrt{5}}$+2$\sqrt{20}$-$\sqrt{45}$+$\sqrt{\frac{1}{2}}$
=5$\sqrt{2}-\frac{\sqrt{5}}{5}$$+4\sqrt{5}$-3$\sqrt{5}$$+\frac{\sqrt{2}}{2}$
=$\frac{11}{2}\sqrt{2}$$+\frac{4}{5}\sqrt{5}$
(2)($\sqrt{18}$-3$\sqrt{\frac{1}{2}}$)×$\sqrt{6}$
=$\sqrt{18}$×$\sqrt{6}$-3$\sqrt{\frac{1}{2}}$×$\sqrt{6}$
=6$\sqrt{3}-3\sqrt{3}$
=$3\sqrt{3}$
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.

练习册系列答案
相关题目
17.下列事件是随机事件的是( )
| A. | 没有水分,种子发芽 | B. | 小张买了一张彩票中500万大奖 | ||
| C. | 抛一枚骰子,正面向上的点数是7 | D. | 367人中至少有2人的生日相同 |
1.一个n边形的内角和比它的外角和至少大120°,则n的最小值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
18.函数y=$\sqrt{x-3}$中自变量x的取值范围是( )
| A. | x≤3 | B. | x≠3 | C. | x≠-3 | D. | x≥3 |
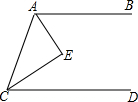 如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是互相垂直.
如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是互相垂直.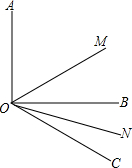 (1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;