题目内容
 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE于点E,AD⊥CE于点D.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE于点E,AD⊥CE于点D.求证:(1)△BEC≌△CDA;
(2)DE=AD-BE.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)易证∠CAD=∠BCE,即可证明△CDA≌△BEC,即可解题;
(2)根据(1)中结论可得CD=BE,CE=AD,根据DE=CE-CD,即可解题.
(2)根据(1)中结论可得CD=BE,CE=AD,根据DE=CE-CD,即可解题.
解答:证明:(1)∵∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
在△CDA和△BEC中,
,
∴△CDA≌△BEC(AAS);
(2)∵△CDA≌△BEC,
∴CD=BE,CE=AD,
∵DE=CE-CD,
∴DE=AD-BE.
∴∠CAD=∠BCE,
在△CDA和△BEC中,
|
∴△CDA≌△BEC(AAS);
(2)∵△CDA≌△BEC,
∴CD=BE,CE=AD,
∵DE=CE-CD,
∴DE=AD-BE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CDA≌△BEC是解题的关键.

练习册系列答案
相关题目
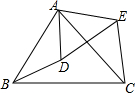 如图,D为△ABC内一点,E为△ABC外一点,且满足
如图,D为△ABC内一点,E为△ABC外一点,且满足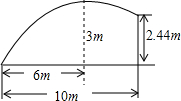 如图,在一次足球训练中,球员小王从球门前方10m起脚射门,球的运行路线恰是一条抛物线,当球飞行的水平距离是6m时,球到达最高点,此时球高约3m.已知球门高2.44m.问此球能否射进球门?
如图,在一次足球训练中,球员小王从球门前方10m起脚射门,球的运行路线恰是一条抛物线,当球飞行的水平距离是6m时,球到达最高点,此时球高约3m.已知球门高2.44m.问此球能否射进球门? 如图,在直角坐标系中,矩形ABC0的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.求E点的坐标.
如图,在直角坐标系中,矩形ABC0的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.求E点的坐标. 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和D(5,0).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和D(5,0).